题目内容
如图,正方形 的边长为2.
的边长为2.
(1)在其四边或内部取点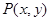 ,且
,且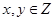 ,求事件:“
,求事件:“ ”的概率;
”的概率;
(2)在其内部取点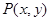 ,且
,且 ,求事件“
,求事件“ 的面积均大于
的面积均大于 ”的概率.
”的概率.
(1) (2)
(2)
解析试题分析:解:
(1)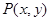 共9种情形:
共9种情形: 3分
3分
满足 ,即
,即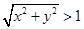 ,共有6种 -5分
,共有6种 -5分
因此所求概率为 6分
6分
(2)设 到
到 的距离为
的距离为 ,则
,则 ,即
,即 8分
8分 到
到 、
、 、
、 、
、 的距离均大于
的距离均大于 9分
9分 概率为
概率为 - 12分
- 12分
考点:几何概型和古典概型
点评:解决的关键是能够准确根据两个重要的概率模型来求解概率值,属于基础题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件,测量产品中的微量元素 ,
, 的含量(单位:毫克)下表是乙厂的5件产品的测量数据:
的含量(单位:毫克)下表是乙厂的5件产品的测量数据:
| 编号 | 1 | 2 | 3 | 4 | 5 |
 | 160 | 178 | 166 | 175 | 180 |
 | 75 | 80 | 77 | 70 | 81 |
(2)若
 且
且 为次品,从乙厂抽出的上述5件产品中,有放回的随机抽取1件产品,抽到次品则停止抽取,否则继续抽取,直到抽出次品为止,但抽取次数最多不超过3次,求抽取次数
为次品,从乙厂抽出的上述5件产品中,有放回的随机抽取1件产品,抽到次品则停止抽取,否则继续抽取,直到抽出次品为止,但抽取次数最多不超过3次,求抽取次数 的分布列及数学期望.
的分布列及数学期望. (本小题满分12分)
甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在8,9,10环,且每次射击击中与否互不影响.甲、乙射击命中环数的概率如表:
| | 8环 | 9环 | 10环 |
| 甲 | 0.2 | 0.45 | 0.35 |
| 乙 | 0.25 | 0.4 | 0.35 |
(Ⅱ)若甲、乙两运动员各自射击2次,求这4次射击中恰有3次击中9环以上(含9环)的概率.

 ,求
,求 ,求:
,求: 上的概率;
上的概率;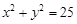 外的概率。
外的概率。 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为 ;两人租车时间都不会超过四小时。
;两人租车时间都不会超过四小时。 ,求
,求
 是锐角三角形的概率。
是锐角三角形的概率。