题目内容
已知体积为
的正三棱锥P-ABC的外接球的球心为O，若满足
，则此三棱锥外接球的半径是（ ）A．2
B．
C．
D．
【答案】分析：由题意球的三角形ABC的位置，以及形状，利用球的体积，求出球的半径即可．
解答：解：正三棱锥D-ABC的外接球的球心O满足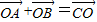
，
说明三角形ABC在球O的大圆上，并且为正三角形，
设球的半径为：R，棱锥的底面正三角形ABC的高为：
底面三角形ABC的边长为：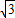
R
正三棱锥的体积为：
×
×（ 
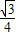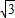R）2×R=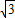
解得R3=4，则此三棱锥外接球的半径是R=
故选D．
点评：本题考查球的内接体问题、棱锥的体积，考查空间想象能力，是中档题．
解答：解：正三棱锥D-ABC的外接球的球心O满足
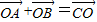，说明三角形ABC在球O的大圆上，并且为正三角形，
设球的半径为：R，棱锥的底面正三角形ABC的高为：
底面三角形ABC的边长为：
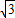R正三棱锥的体积为：
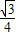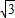××（ R）2×R=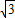解得R3=4，则此三棱锥外接球的半径是R=
故选D．
点评：本题考查球的内接体问题、棱锥的体积，考查空间想象能力，是中档题．
练习册系列答案
相关题目
的正三棱锥P-ABC的外接球的球心为O，若满足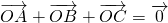
，则此三棱锥外接球的半径是
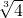
的正三棱锥V-ABC的外接球的球心为O，满足
，则该三棱锥外接球的体积为 ．
的正三棱锥V-ABC的外接球的球心为O，满足
，则该三棱锥外接球的体积为 ．
的正三棱锥
的外接球的球心为
，若满足
,则此三棱锥外接球的半径是（
）
B.
C.
D. 