Question

(本小题满分12分)

       如图，在四棱锥P—ABCD中，底面ABCD是矩形，PA⊥平面ABCD，AP=AB，BP=BC=2，E，F分别是PB,PC的中点.

       (Ⅰ)证明：EF∥平面PAD；

       (Ⅱ)求三棱锥E—ABC的体积V.

 

Answer 1

【答案】

(Ⅰ)证明见解析

(Ⅱ) V_E-ABC=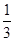

【解析】本题主要考查立体几何中点线面位置关系，并以我们熟悉的四棱锥为载体，尽管侧重推理和运算，但所用知识点不多，运算也不麻烦，对于大多考生来说还是一道送分题．

(Ⅰ) 在△PBC中，E，F分别是PB，PC的中点，∴EF∥BC.

       又BC∥AD，∴  EF∥AD,

       又∵AD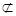平面PAD，EF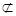平面PAD,[来源:]

       ∴EF∥平面PAD.

 (Ⅱ)连接AE，AC，EC，过E作EG∥PA交AB于点G,

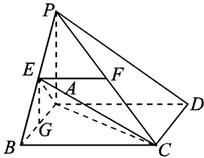
       则EG⊥平面ABCD,且EG=PA.

       在△PAB中，AP=AB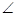，PAB=90°,BP=2，∴AP=AB=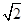,EG=.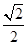

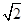       ∴S_△ABC=AB·BC=××2=,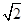

       ∴V_E-ABC=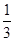S_△ABC·EG=××=.

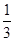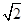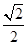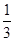点评：本题是我们常见的题型，相比平时那些求角及距离的题要容易的多，并且所考知识点不多运算也不麻烦，是一道基础题．