题目内容
为了得到y=f(-2x)的图象,可以把函数y=f(1-2x)的图象按向量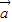 进行平移,则
进行平移,则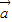 等于( )
等于( )A.(1,0)
B.(-1,0)
C.
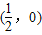
D.
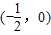
【答案】分析:我们设平移向量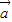 =(h,k),根据函数图象的“左加右减,上加下减”的平移法则,我们可根据平移前函数的解析式为y=f(1-2x),平移后函数的解析式为y=f(-2x),构造出关于h,k的方程组,解方程组即可得到平移向量
=(h,k),根据函数图象的“左加右减,上加下减”的平移法则,我们可根据平移前函数的解析式为y=f(1-2x),平移后函数的解析式为y=f(-2x),构造出关于h,k的方程组,解方程组即可得到平移向量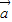 的坐标.
的坐标.
解答:解:设平移向量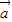 =(h,k)
=(h,k)
则函数y=f(1-2x)的图象按向量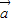 进行平移后所得函数的解析式为
进行平移后所得函数的解析式为
y=f[1-2(x-h)]+k=f(-2x+1+2h)+k=f(-2x)
即1+2h=0,k=0
解得h=- ,k=0
,k=0
故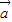 =(-
=(- ,0)
,0)
故选D
点评:本题考查的知识点是函数的图象与图象变化,其中根据平移前函数的解析式和平移后函数的解析式,构造出关于平移向量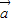 坐标h,k的方程组,是解答此类问题的关键.
坐标h,k的方程组,是解答此类问题的关键.
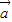 =(h,k),根据函数图象的“左加右减,上加下减”的平移法则,我们可根据平移前函数的解析式为y=f(1-2x),平移后函数的解析式为y=f(-2x),构造出关于h,k的方程组,解方程组即可得到平移向量
=(h,k),根据函数图象的“左加右减,上加下减”的平移法则,我们可根据平移前函数的解析式为y=f(1-2x),平移后函数的解析式为y=f(-2x),构造出关于h,k的方程组,解方程组即可得到平移向量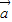 的坐标.
的坐标.解答:解:设平移向量
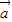 =(h,k)
=(h,k)则函数y=f(1-2x)的图象按向量
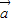 进行平移后所得函数的解析式为
进行平移后所得函数的解析式为y=f[1-2(x-h)]+k=f(-2x+1+2h)+k=f(-2x)
即1+2h=0,k=0
解得h=-
 ,k=0
,k=0故
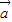 =(-
=(- ,0)
,0)故选D
点评:本题考查的知识点是函数的图象与图象变化,其中根据平移前函数的解析式和平移后函数的解析式,构造出关于平移向量
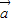 坐标h,k的方程组,是解答此类问题的关键.
坐标h,k的方程组,是解答此类问题的关键. 
练习册系列答案
相关题目
 函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<| π |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
 (2012•包头一模)函数f(x)=sin(ωx+?)(其中
(2012•包头一模)函数f(x)=sin(ωx+?)(其中 函数f(x)=sin(ωx+φ)(其中
函数f(x)=sin(ωx+φ)(其中 函数f(x)=Asin(ωx+?)(其中A>0,ω>0,
函数f(x)=Asin(ωx+?)(其中A>0,ω>0, (2011•焦作一模)已知函数f(x)的图象过点(
(2011•焦作一模)已知函数f(x)的图象过点(