题目内容
(本题满分10分)设函数 ,
,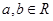
(1)若函数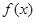 在
在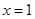 处与直线
处与直线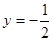 相切;
相切;
①求实数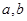 的值;②求函数
的值;②求函数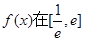 上的最大值;
上的最大值;
(2)当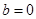 时,若不等式
时,若不等式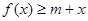 对所有的
对所有的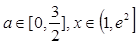 都成立,求实数
都成立,求实数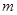 的取值范围.
的取值范围.
【答案】
解:(1)①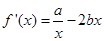 ∵函数
∵函数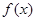 在
在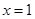 处与直线
处与直线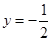 相切
相切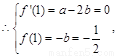 解得
解得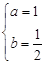 …………2分
…………2分
②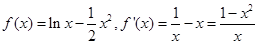
当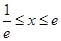 时,令
时,令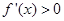 得
得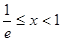 ;
;
令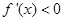 ,得
,得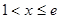
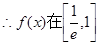 上单调递增,在[1,e]上单调递减,
上单调递增,在[1,e]上单调递减,
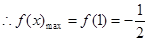 …………6分
…………6分
(2)当b=0时,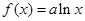 若不等式
若不等式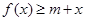 对所有的
对所有的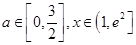 都成立,
都成立,
则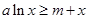 对所有的
对所有的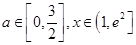 都成立,
都成立,
即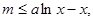 对所有的
对所有的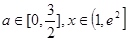 都成立,
都成立,
令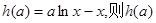 为一次函数,
为一次函数,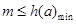
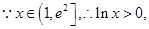
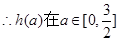 上单调递增
上单调递增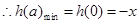 ,
,
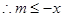 对所有的
对所有的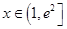 都成立。
都成立。
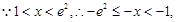
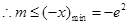 ----------------------------------10分
----------------------------------10分
(注:也可令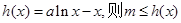 所有的
所有的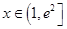 都成立,分类讨论得
都成立,分类讨论得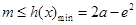 对所有的
对所有的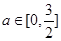 都成立,
都成立,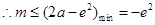 ,请根据过程酌情给分)
,请根据过程酌情给分)
【解析】略

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 ,
,
 在
在 处与直线
处与直线 相切;
相切; 的值;②求函数
的值;②求函数 上的最大值;
上的最大值; 时,若不等式
时,若不等式 对所有的
对所有的 都成立,求实数
都成立,求实数 的取值范围.
的取值范围. .
. ,(a¹0,a、bÎR)恒成立,求实数x的范围.
,(a¹0,a、bÎR)恒成立,求实数x的范围.
 为奇函数,其图象在点
为奇函数,其图象在点 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数 的最小值为
的最小值为 .试求
.试求 ,
, ,
, 的值。
的值。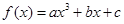
 为奇函数,其图象在点
为奇函数,其图象在点 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数 的最小值为
的最小值为 .试求
.试求 ,
, ,
, 的值。
的值。 的内角A、B、C所对的边长分别为
的内角A、B、C所对的边长分别为 ,且
,且 ,
, 。
。 时,求
时,求 的值.
的值. 的值.
的值.