题目内容
已知![]() =(c,o)(c>o),
=(c,o)(c>o),![]() =(
=(![]() ,
,![]() )(
)(![]() R),
R),![]() 的最小值为1,若动点P同时满足下列三个条件:①
的最小值为1,若动点P同时满足下列三个条件:①![]() ;②
;②![]() ,其中
,其中![]() R;③动点P的轨迹C经过点B(0,一1).
R;③动点P的轨迹C经过点B(0,一1).
(1)求![]() 的值;
的值;
(2)求曲线C的方程;
(3)是否存在方向向量为![]() ≠0)的直线
≠0)的直线![]() ,使
,使![]() 与曲线C交于两个不同的点M、N,且
与曲线C交于两个不同的点M、N,且![]() ?若存在,求出k的取值范围;若不存在,请说明理由.
?若存在,求出k的取值范围;若不存在,请说明理由.
解:(1)解法一:![]()
= ,
,
当![]() 时,
时,![]() ,所以
,所以![]() .
.
解法二:设G(![]() ,y),则G在直线
,y),则G在直线![]() 上,
上,
所以![]() 的最小值为点F到直线
的最小值为点F到直线![]() 的距离,即
的距离,即![]() ,得
,得![]() .
.
(2)∵![]() ,∴PE垂直于直线
,∴PE垂直于直线![]()
又![]() .
.
∴点P在以F为焦点、![]() 为准线的椭圆上.
为准线的椭圆上.
设P![]() ,则有
,则有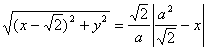 ,
,
点B(0,-1)代入,解得![]() .
.
∴曲线C的方程为![]() .
.
(3)假设存在方向向量为![]() 的直线
的直线![]() 满足条件,则可设
满足条件,则可设![]() :
:![]() ,与椭圆
,与椭圆![]() 联立,
联立,
消去y得![]() .
.
由判别式△>0,可得![]() ①
①
设M(![]() ),N(
),N(![]() ),MN的中点P(
),MN的中点P(![]() ),
),
由|BM|=|BN|,则有BP⊥MN.
由韦达定理代入![]() ,可得到
,可得到![]() ②
②
联立①②,可得到![]() ,
,
∵![]() ,∴
,∴![]() 或
或![]() .
.
即存在![]() ∈(-1,0)∪(0,1),使
∈(-1,0)∪(0,1),使![]() 与曲线C交于两个不同的点M、N,且
与曲线C交于两个不同的点M、N,且![]() .
.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
设A1,A2,A3,A4是平面直角坐标系中两两不同的四点,若
=λ
(λ∈R),
=μ
(μ∈R),且
+
=2,则称A3,A4调和分割A1,A2,已知点C(c,0),D(d,O)(c,d∈R)调和分割点A(0,0),B(1,0),则下面说法正确的是( )
| A1A3 |
| A1A2 |
| A1A4 |
| A1A2 |
| 1 |
| λ |
| 1 |
| μ |
| A、C可能是线段AB的中点 |
| B、D可能是线段AB的中点 |
| C、C,D可能同时在线段AB上 |
| D、C,D不可能同时在线段AB的延长线上 |
 如图,已知C是⊙O的直径AB的延长线上的一点,D是⊙O上的一点且AD=CD,∠C=30°,求证:DC是⊙O的切线.
如图,已知C是⊙O的直径AB的延长线上的一点,D是⊙O上的一点且AD=CD,∠C=30°,求证:DC是⊙O的切线. 如图,已知:椭圆M的中心为O,长轴的两个端点为A、B,右焦点为F,AF=5BF.若椭圆M经过点C,C在AB上的射影为F,且△ABC的面积为5.
如图,已知:椭圆M的中心为O,长轴的两个端点为A、B,右焦点为F,AF=5BF.若椭圆M经过点C,C在AB上的射影为F,且△ABC的面积为5.