题目内容
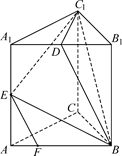
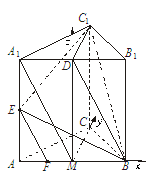
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥面ABC,D、E分别是棱A1B1、AA1的中点,点F在棱AB上,且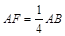 .
.
(Ⅰ)求证:EF∥平面BDC1;
(Ⅱ)求二面角E-BC1-D的余弦值.
(Ⅰ)取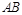 的中点M,
的中点M,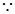
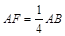
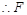 为
为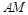 的中点,又
的中点,又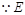 为
为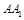 的中点,∴
的中点,∴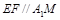 在三棱柱
在三棱柱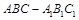 中,
中,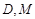 分别为
分别为 的中点,
的中点,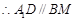 ,且
,且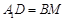 则四边形A1DBM为平行四边形,
则四边形A1DBM为平行四边形,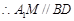
 ,又
,又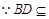 平面
平面 ,
,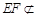 平面
平面
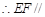 平面
平面 (Ⅱ)
(Ⅱ)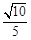
解析试题分析:取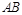 的中点M,
的中点M,
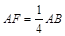 ,
,
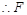 为
为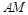 的中点,又
的中点,又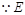 为
为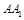 的中点,∴
的中点,∴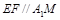 ,
,
在三棱柱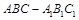 中,
中,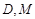 分别为
分别为 的中点,
的中点,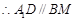 ,且
,且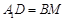 ,
,
则四边形A1DBM为平行四边形,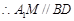 ,
, ,又
,又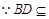 平面
平面 ,
,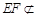 平面
平面 ,
,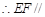 平面
平面 . 6分
. 6分
(Ⅱ)连接DM,分别以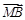 、
、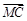 、
、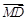 所在直线为x轴、y轴、z轴,建立如图空间直角坐标系,则
所在直线为x轴、y轴、z轴,建立如图空间直角坐标系,则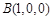 ,
,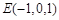 ,
,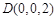 ,
, ,
,
∴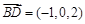 ,
,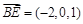 ,
,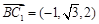 .
.
设面BC1D的一个法向量为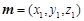 ,面BC1E的一个法向量为
,面BC1E的一个法向量为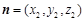 ,
,
则由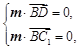 得
得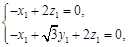 取
取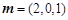 ,
,
又由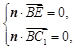 得
得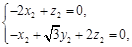 取
取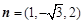 ,
,
则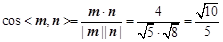 ,
,
故二面角E-BC1-D的余弦值为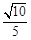 . 12分
. 12分
考点:线面平行的判定及二面角求解
点评:利用空间向量法证明线面平行只需证明直线的方向向量与平面的法向量垂直且直线不在面内即可,求二面角时首先找到两面的法向量,求出法向量的夹角,观察图形得到二面角(等于夹角或与夹角互补)

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
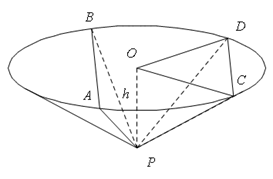
 .底面圆心为
.底面圆心为 ,其母线与底面所成的角为
,其母线与底面所成的角为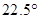 .
.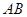 和
和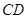 是底面圆
是底面圆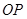 与平面
与平面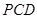 所成的角为
所成的角为 ,
, 
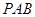 与平面
与平面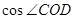 .
.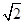 。
。
 的值;若不存在,说明理由.
的值;若不存在,说明理由.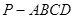 中,
中,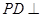 底面
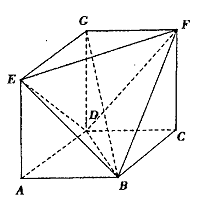
底面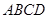 ,面
,面 为侧棱
为侧棱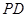 上一点.该四棱锥的俯视图和侧(左)视图如图2所示.
上一点.该四棱锥的俯视图和侧(左)视图如图2所示. 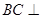 平面
平面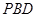 ;
; 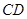 上是否存在点
上是否存在点 ,使
,使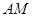 与
与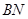 所成角的余弦值为
所成角的余弦值为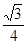 ?若存在,找到所有符合要求的点
?若存在,找到所有符合要求的点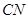 的长;若不存在,说明理由.
的长;若不存在,说明理由.
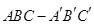 ,
,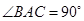 ,
,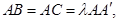 点M,N分别为
点M,N分别为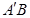 和
和 的中点.
的中点.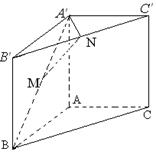
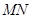 ∥平面
∥平面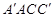 ;
;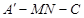 A为直二面角,求
A为直二面角,求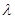 的值.
的值. 平面ABCD,
平面ABCD, ,E是PC上的一点.
,E是PC上的一点.
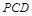 ;
;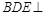 平面
平面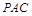 ;
; 为多长时,
为多长时, 平面
平面 ?
?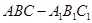 的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,
的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,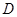 为
为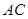 的中点.
的中点.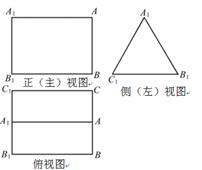
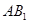 ∥平面
∥平面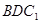 ;
;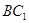 ,且
,且 ,求点
,求点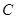 到平面
到平面 的距离.
的距离. ,E、F分别为线段PD和BC的中点.
,E、F分别为线段PD和BC的中点.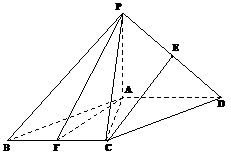
 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.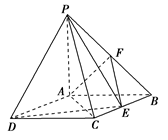
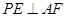 ;
;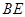 为何值时,
为何值时,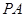 与平面
与平面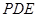 所成角的大小为45°.
所成角的大小为45°.