题目内容
曲线C是中心在原点,焦点在x轴上的双曲线的右支,已知它的右准线方程为l: ,一条渐近线方程是
,一条渐近线方程是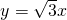 ,线段PQ是过曲线C右焦点F的一条弦,R是弦PQ的中点.
,线段PQ是过曲线C右焦点F的一条弦,R是弦PQ的中点.
(1)求曲线C的方程;
(2)当点P在曲线C上运动时,求点R到y轴距离的最小值;
(3)若在直线l的左侧能作出直线m:x=a,使点R在直线m上的射影S满足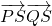 =0.当点P在曲线C上运动时,求a的取值范围.
=0.当点P在曲线C上运动时,求a的取值范围.
解:(1)设双曲线C的方程为: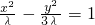 (x
(x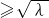 ),λ>0
),λ>0
则它的右准线方程为x=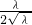 =
=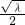
由已知可得,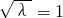
∴λ=1
故所求双曲线方程为 (x≥1)
(x≥1)
(2)由(1)知,曲线C的右焦点F(2,0)
若弦PQ的斜率存在,则弦PQ的方程y=k(x-2),代入双曲线方程可得
(3-k2)x2+4k2x-4k2-3=0
设P(x1,y1),Q(x2,y2)
则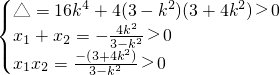
解得:k2>3,
点R到y轴距离: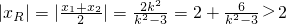
而当弦PQ的斜率不存在时,点R到y轴距离|xR|=2.
所以点R到y轴距离的最小值为2.…8′
(3)∵点R在直线m上的射影S满足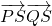 =0,
=0,
 …①
…①
∵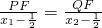
∴PQ=PF+QF=2(x1+x2-1)=4xR-2②
②代入①可得2xR-1=xR-a
∴xR=1-a
∵|xR|≥2,a
∴a≤-1
分析:(1)由渐近线方程可设双曲线C的方程为: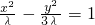 (x
(x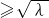 ),λ>0然后根据准线方程可求λ,即可求解
),λ>0然后根据准线方程可求λ,即可求解
(2)由(1)知F,设处出弦PQ的方程y=k(x-2),代入双曲线方程,根据方程的根与系数关系可求k的范围,然后根据点R到y轴距离及所求k的范围即可求解;当弦PQ的斜率不存在时,点R到y轴距离容易求解
(3)由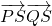 =0,可知△PSR为直角三角形,可求R到直线m的距离,结合双曲线的焦半径公式可得xR与a之间的关系,结合|xR|≥2,a
=0,可知△PSR为直角三角形,可求R到直线m的距离,结合双曲线的焦半径公式可得xR与a之间的关系,结合|xR|≥2,a 可求
可求
点评:本题主要考查了由双曲线的性质求解双曲线方程,直线与双曲线的相交关系的应用,方程的根与系数关系的应用是求解直线与曲线相交关系常用的方法
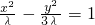 (x
(x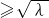 ),λ>0
),λ>0则它的右准线方程为x=
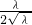 =
=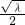
由已知可得,
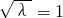
∴λ=1
故所求双曲线方程为
 (x≥1)
(x≥1)(2)由(1)知,曲线C的右焦点F(2,0)
若弦PQ的斜率存在,则弦PQ的方程y=k(x-2),代入双曲线方程可得
(3-k2)x2+4k2x-4k2-3=0
设P(x1,y1),Q(x2,y2)
则
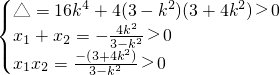
解得:k2>3,
点R到y轴距离:
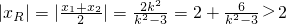
而当弦PQ的斜率不存在时,点R到y轴距离|xR|=2.
所以点R到y轴距离的最小值为2.…8′
(3)∵点R在直线m上的射影S满足
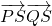 =0,
=0, …①
…①∵
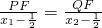
∴PQ=PF+QF=2(x1+x2-1)=4xR-2②
②代入①可得2xR-1=xR-a
∴xR=1-a
∵|xR|≥2,a

∴a≤-1
分析:(1)由渐近线方程可设双曲线C的方程为:
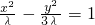 (x
(x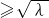 ),λ>0然后根据准线方程可求λ,即可求解
),λ>0然后根据准线方程可求λ,即可求解(2)由(1)知F,设处出弦PQ的方程y=k(x-2),代入双曲线方程,根据方程的根与系数关系可求k的范围,然后根据点R到y轴距离及所求k的范围即可求解;当弦PQ的斜率不存在时,点R到y轴距离容易求解
(3)由
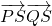 =0,可知△PSR为直角三角形,可求R到直线m的距离,结合双曲线的焦半径公式可得xR与a之间的关系,结合|xR|≥2,a
=0,可知△PSR为直角三角形,可求R到直线m的距离,结合双曲线的焦半径公式可得xR与a之间的关系,结合|xR|≥2,a 可求
可求点评:本题主要考查了由双曲线的性质求解双曲线方程,直线与双曲线的相交关系的应用,方程的根与系数关系的应用是求解直线与曲线相交关系常用的方法

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目