题目内容
（如图）过椭圆
+
=1（a＞b＞0）的左焦点F任作一条与两坐标轴都不垂直的弦AB；若点M在x
轴上，且使得MF为△AMB的一条内角平分线，则称点M为该椭圆的“左特征点”．
（1）求椭圆
+y2=1的“左特征点”M的坐标．
（2）试根据（1）中的结论猜测：椭圆
+
=1（a＞b＞0）的“左特征点”M是一个怎么样的点？并证明你的结论．
| x2 |
| a2 |
| y2 |
| b2 |
轴上，且使得MF为△AMB的一条内角平分线，则称点M为该椭圆的“左特征点”．（1）求椭圆
| x2 |
| 5 |
（2）试根据（1）中的结论猜测：椭圆
| x2 |
| a2 |
| y2 |
| b2 |
分析：（1）设M(m，0)为椭圆
+y2=1的左特征点，由椭圆左焦点F（-2，0），可设直线AB方程为x=ky-2（k≠0），代入
+y2=1，得（k2+5）y2-4ky-1=0，由∠AMB被x轴平分，kAM+kBM=0，即
+
=0整理可求．
（2）对于椭圆
+y2=1，a=
，b=1，c=2，结合椭圆的性质特征可猜想：椭圆
+
=1的左特征点是椭圆的左准线与x轴的交点，然后可以利用第二定义给与证明．
| x2 |
| 5 |
| x2 |
| 5 |
| y1 |
| x1-m |
| y2 |
| x2-m |
（2）对于椭圆
| x2 |
| 5 |
| 5 |
| x2 |
| a2 |
| y2 |
| b2 |
解答：解：（1）设M(m，0)为椭圆
+y2=1的左特征点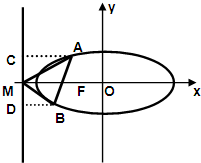
因为，椭圆的左焦点F（-2，0），
可设直线AB的方程为x=ky-2（k≠0）
代入
+y2=1，得：（ky-2）y2+5y2=5，
即（k2+5）y2-4ky-1=0，设A（x1，y1），B（x2，y2）得y1+y2=
，y1y2=-
由于，∠AMB被x轴平分，kAM+kBM=0，即
+
=0y1（x2-m）+y2（x1-m）=0，即y1（ky2-2）+y2（ky1-2）-（y1+y2）m=0
所以，2ky1y2-（y1+y2）（m+2）=0
于是，2k(-
)-
(m+2)=
=0
因为k≠0，所以1+2（m+2）=0，即m=-
M=(-
，0)
（2）对于椭圆
+y2=1，a=
，b=1，c=2，-
=-
于是猜想：椭圆
+
=1的“左特征点”是椭圆的左准线与x轴的交点
证明：设椭圆的左准线l与x轴相交于M点，过A、B分别作l的垂线，
垂足为C、D．
据椭圆的第二定义：
=
，即
=
由于AC∥FM∥BD，所以
=
于是
=
，即
=
所以，∠AMC=∠BMD⇒∠AMF=∠BMF
则MF为∠AMB的平分线
故M为椭圆的“左特征点”．
| x2 |
| 5 |
因为，椭圆的左焦点F（-2，0），
可设直线AB的方程为x=ky-2（k≠0）
代入
| x2 |
| 5 |
即（k2+5）y2-4ky-1=0，设A（x1，y1），B（x2，y2）得y1+y2=
| 4k |
| k2+5 |
| 1 |
| k2+5 |
由于，∠AMB被x轴平分，kAM+kBM=0，即
| y1 |
| x1-m |
| y2 |
| x2-m |
所以，2ky1y2-（y1+y2）（m+2）=0
于是，2k(-
| 1 |
| k2+5 |
| 4k |
| k2+5 |
| -2k[1+2(m+2)] |
| k2+5 |
因为k≠0，所以1+2（m+2）=0，即m=-
| 5 |
| 2 |
| 5 |
| 2 |
（2）对于椭圆
| x2 |
| 5 |
| 5 |
| a2 |
| c |
| 5 |
| 2 |
于是猜想：椭圆
| x2 |
| a2 |
| y2 |
| b2 |
证明：设椭圆的左准线l与x轴相交于M点，过A、B分别作l的垂线，
垂足为C、D．
据椭圆的第二定义：
| |AF| |
| |AC| |
| |BF| |
| |BD| |
| |AF| |
| |BF| |
| |AC| |
| |BD| |
由于AC∥FM∥BD，所以
| |AF| |
| |BF| |
| |CM| |
| |DM| |
于是
| |AC| |
| |BD| |
| |CM| |
| |DM| |
| |AC| |
| |CM| |
| |BD| |
| |DM| |
所以，∠AMC=∠BMD⇒∠AMF=∠BMF
则MF为∠AMB的平分线
故M为椭圆的“左特征点”．
点评：本题以新定义为载体主要考查了椭圆性质的应用，直线与椭圆相交关系的处理，要注意解题中直线AB得方程设为x=ky-2（k≠0）的好处在于避免讨论直线的斜率是否存在．
练习册系列答案
相关题目
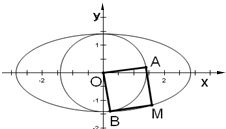如图，过椭圆C：
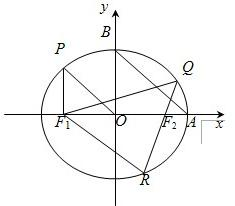如图，过椭圆
（2003•朝阳区一模）已知：如图，过椭圆C：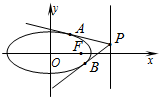
已知椭圆的中心在坐标原点，焦点在x轴上，并且焦距为2，短轴与长轴的比是