Question

（本小题满分12分）

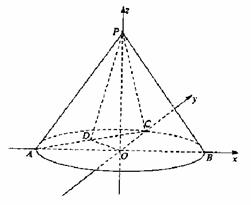
如图5，在圆锥中，已知=，⊙O的直径,是的中点，为的中点．

（Ⅰ）证明：平面 平面;

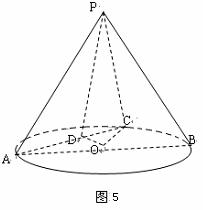（Ⅱ）求二面角的余弦值。

Answer 1

解法1：连结OC，因为

又底面⊙O，AC底面⊙O，所以，

因为OD，PO是平面POD内的两条相交直线，所以平面POD，

而平面PAC，所以平面POD平面PAC。

（II）在平面POD中，过O作于H，由（I）知，平面

_{所以平面PAC，又面PAC，所以}

_{在平面PAO中，过O作于G，}

    连接HG，

则有平面OGH，

从而，故为二面角B—PA—C的平面角。

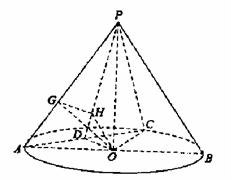在

在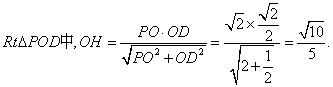

在

在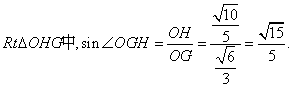

所以

故二面角B—PA—C的余弦值为

解法2：（I）如图所示，以O为坐标原点，OB、OC、OP所在直线分别为x轴、y轴，z轴建立空间直角坐标系，则

，

设是平面POD的一个法向量，

则由，得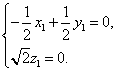

所以

设是平面PAC的一个法向量，

则由，

得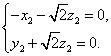

所以

得。

因为

所以从而平面平面PAC。

（II）因为y轴平面PAB，所以平面PAB的一个法向量为

由（I）知，平面PAC的一个法向量为

设向量的夹角为，则

由图可知，二面角B—PA—C的平面角与相等，

所以二面角B—PA—C的余弦值为