题目内容
(本题满分15分)
男运动员6名,女运动员4名,其中男女队长各1人,从中选5人外出比赛,
分别求出下列情形有多少种选派方法?(以数字作答)
(1)男3名,女2名;
(2)队长至少有1人参加;
(3)至少1名女运动员;
(4)既要有队长,又要有女运动员.
男运动员6名,女运动员4名,其中男女队长各1人,从中选5人外出比赛,
分别求出下列情形有多少种选派方法?(以数字作答)
(1)男3名,女2名;
(2)队长至少有1人参加;
(3)至少1名女运动员;
(4)既要有队长,又要有女运动员.
(1)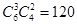 种选法.(2)
种选法.(2)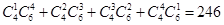 种选法.
种选法.
(3)196种选法.(4)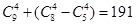 种.
种.
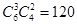 种选法.(2)
种选法.(2)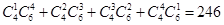 种选法.
种选法.(3)196种选法.(4)
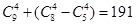 种.
种. 第一问中,要确定所有的选法由题意知本题是一个分步计数问题,
首先选3名男运动员,有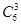 种选法.
种选法.
再选2名女运动员,有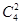 C42种选法
C42种选法
第二问中,(间接法):“至少1名女运动员”的反面为“全是男运动员”.
从10人中任选5人,有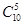 种选法,其中全是男运动员的选法有
种选法,其中全是男运动员的选法有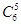 种.
种.
第三问中,“只有男队长”的选法为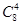 种;
种;
“只有女队长”的选法为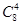 种;
种;
“男、女队长都入选”的选法为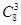 种;
种;
第四问中当有女队长时,其他人选法任意,共有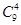 种选法.
种选法.
不选女队长时,必选男队长,共有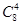 种选法.
种选法.
其中不含女运动员的选法有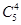 种,
种,
解:(1)由题意知本题是一个分步计数问题,
首先选3名男运动员,有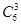 种选法.
种选法.
再选2名女运动员,有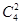 C42种选法.
C42种选法.
共有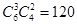 种选法.
种选法.
(3分)
(2)法一(直接法):“至少1名女运动员”包括以下几种情况:
1女4男,2女3男,3女2男,4女1男.
由分类加法计数原理可得有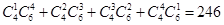 种选法.
种选法.
法二(间接法):“至少1名女运动员”的反面为“全是男运动员”.
从10人中任选5人,有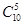 种选法,其中全是男运动员的选法有
种选法,其中全是男运动员的选法有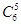 种.
种.
所以“至少有1名女运动员”的选法有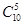 -
-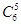 =246种. (4分)
=246种. (4分)
(3)“只有男队长”的选法为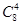 种;
种;
“只有女队长”的选法为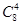 种;
种;
“男、女队长都入选”的选法为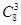 种;
种;
∴共有2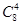 +
+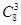 =196种.
=196种.
∴“至少1名队长”的选法有C105-C85=196种选法. (4分)
(4)当有女队长时,其他人选法任意,共有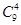 种选法.
种选法.
不选女队长时,必选男队长,共有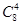 种选法.
种选法.
其中不含女运动员的选法有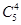 种,
种,
∴不选女队长时共有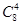 -
-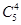 种选法.
种选法.
既有队长又有女运动员的选法共有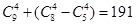 种. (4分)
种. (4分)
首先选3名男运动员,有
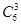 种选法.
种选法.再选2名女运动员,有
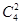 C42种选法
C42种选法第二问中,(间接法):“至少1名女运动员”的反面为“全是男运动员”.
从10人中任选5人,有
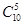 种选法,其中全是男运动员的选法有
种选法,其中全是男运动员的选法有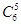 种.
种.第三问中,“只有男队长”的选法为
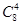 种;
种;“只有女队长”的选法为
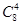 种;
种;“男、女队长都入选”的选法为
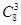 种;
种;第四问中当有女队长时,其他人选法任意,共有
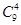 种选法.
种选法.不选女队长时,必选男队长,共有
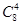 种选法.
种选法.其中不含女运动员的选法有
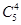 种,
种,解:(1)由题意知本题是一个分步计数问题,
首先选3名男运动员,有
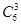 种选法.
种选法.再选2名女运动员,有
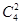 C42种选法.
C42种选法.共有
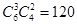 种选法.
种选法.(3分)
(2)法一(直接法):“至少1名女运动员”包括以下几种情况:
1女4男,2女3男,3女2男,4女1男.
由分类加法计数原理可得有
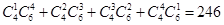 种选法.
种选法.法二(间接法):“至少1名女运动员”的反面为“全是男运动员”.
从10人中任选5人,有
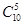 种选法,其中全是男运动员的选法有
种选法,其中全是男运动员的选法有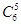 种.
种.所以“至少有1名女运动员”的选法有
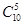 -
-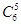 =246种. (4分)
=246种. (4分)(3)“只有男队长”的选法为
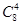 种;
种;“只有女队长”的选法为
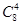 种;
种;“男、女队长都入选”的选法为
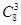 种;
种;∴共有2
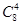 +
+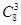 =196种.
=196种.∴“至少1名队长”的选法有C105-C85=196种选法. (4分)
(4)当有女队长时,其他人选法任意,共有
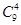 种选法.
种选法.不选女队长时,必选男队长,共有
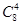 种选法.
种选法.其中不含女运动员的选法有
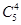 种,
种,∴不选女队长时共有
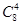 -
-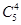 种选法.
种选法.既有队长又有女运动员的选法共有
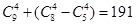 种. (4分)
种. (4分)
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
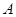 ,
,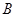 ,
,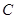 ,
,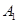 ,
,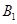 ,
,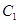 上 各装一个灯泡,要求同一条线段两端的灯泡不同色,则不同的安装方法共有 种(用数字作答).
上 各装一个灯泡,要求同一条线段两端的灯泡不同色,则不同的安装方法共有 种(用数字作答).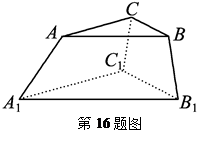
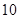 名队员中挑选
名队员中挑选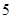 名上场比赛,要求甲、乙中至少有
名上场比赛,要求甲、乙中至少有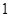 人参加,则下列选派方法种数表示不正确的是( ▲ )
人参加,则下列选派方法种数表示不正确的是( ▲ )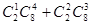
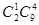
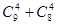
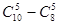
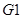 和
和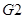 两列列车不在同一小组,如果
两列列车不在同一小组,如果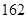 种
种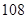 种
种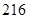 种
种 种
种