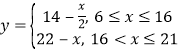题目内容
【题目】如图,抛物线方程为x2=2py(p>0),M为直线y=-2p上任一点,过M引抛物线的切线,切点分别为A,B.求证:A,M,B三点的横坐标成等差数列.
【答案】证明见解析
【解析】
试题由已知可设A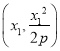 ,B
,B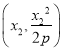 ,M(x0,-2p);求出y′=
,M(x0,-2p);求出y′=![]() 根据导数的几何意义可得kMA=
根据导数的几何意义可得kMA=![]() ,kMB=
,kMB=![]() ;结合M(x0,-2p)得到直线MA的方程为y+2p=
;结合M(x0,-2p)得到直线MA的方程为y+2p=![]() (x-x0),直线MB的方程为y+2p=
(x-x0),直线MB的方程为y+2p=![]() (x-x0),将
(x-x0),将![]() 坐标分别代入对应的直线方程整理可得x0=
坐标分别代入对应的直线方程整理可得x0=![]() ,命题得证.
,命题得证.
试题解析:
由题意设A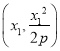 ,B
,B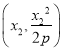 ,
,
M(x0,-2p).由x2=2py,得y=![]() ,则y′=
,则y′=![]() ,
,
所以kMA=![]() ,kMB=
,kMB=![]() .
.
因此直线MA的方程为y+2p=![]() (x-x0).
(x-x0).
直线MB的方程为y+2p=![]() (x-x0).
(x-x0).
又A,B分别在直线MA,MB上,
所以![]() +2p=
+2p=![]() (x1-x0), ①
(x1-x0), ①
![]() +2p=
+2p=![]() (x2-x0), ②
(x2-x0), ②
由①②得![]() ,
,![]() =x1+x2-x0,
=x1+x2-x0,
因此x0=![]() ,
,
所以A,M,B三点的横坐标成等差数列.

练习册系列答案
相关题目