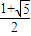题目内容
已知点F(-c,0)(c>0)是双曲线
-
=1的左焦点,过F且平行于双曲线渐近线的直线与圆x2+y2=c2交于点P,且点P在抛物线y2=4cx上,则该双曲线的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
分析:利用抛物线的性质、双曲线的渐近线、直线平行的性质、圆的性质、相似三角形的性质即可得出.
解答:解:如图,设抛物线y2=4cx的准线为l,作PQ⊥l于Q,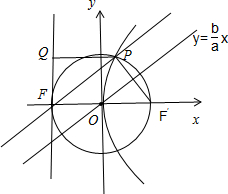
双曲线的右焦点为F',由题意可知FF'为圆x2+y2=c2的直径,
∴PF'⊥PF,且tan∠PFF′=
,|FF'|=2c,
设|PF'|=x,|PF|=y,则
,解得b=2a,
所以4a2=c2-a2,即c2=5a2,所以c=
a,即e=
.
故选B.

双曲线的右焦点为F',由题意可知FF'为圆x2+y2=c2的直径,
∴PF'⊥PF,且tan∠PFF′=
| b |
| a |
设|PF'|=x,|PF|=y,则
|
所以4a2=c2-a2,即c2=5a2,所以c=
| 5 |
| 5 |
故选B.
点评:数列掌握抛物线的性质、双曲线的渐近线、直线平行的性质、圆的性质是解题的关键.

练习册系列答案
相关题目
 如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,若
如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,若 (2006•嘉定区二模)如图,已知点F(1,0),点M在x轴上,点N在y轴上,且
(2006•嘉定区二模)如图,已知点F(1,0),点M在x轴上,点N在y轴上,且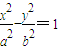 的左焦点,过F且平行于双曲线渐近线的直线与圆x2+y2=c2交于点P,且点P在抛物线y2=4cx上,则该双曲线的离心率是( )
的左焦点,过F且平行于双曲线渐近线的直线与圆x2+y2=c2交于点P,且点P在抛物线y2=4cx上,则该双曲线的离心率是( )