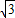题目内容
过点(-3,0)和点(-4, )的直线的倾斜角是
)的直线的倾斜角是
- A.30°
- B.150°
- C.60°
- D.120°
D
分析:设直线的倾斜角是 α,则 0≤α<π,且 tanα=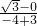 =-
=- ,由此求得α的值.
,由此求得α的值.
解答:设过点(-3,0)和点(-4, )的直线的倾斜角是α,
)的直线的倾斜角是α,
则0≤α<π,且tanα=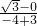 =-
=- ,
,
故 α=120°,
故选 D.
点评:本题考查直线的倾斜角和斜率的关系,以及倾斜角的取值范围,已知三角函数值求角的大小.求出tanα的值,是解题的关键.
分析:设直线的倾斜角是 α,则 0≤α<π,且 tanα=
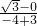 =-
=- ,由此求得α的值.
,由此求得α的值.解答:设过点(-3,0)和点(-4,
 )的直线的倾斜角是α,
)的直线的倾斜角是α,则0≤α<π,且tanα=
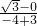 =-
=- ,
,故 α=120°,
故选 D.
点评:本题考查直线的倾斜角和斜率的关系,以及倾斜角的取值范围,已知三角函数值求角的大小.求出tanα的值,是解题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
过点(3,0)和点(4,
)的直线的斜率是( )
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
过点(-3,0)和点(-4,
)的直线的倾斜角是( )
| 3 |
| A、30° | B、150° |
| C、60° | D、120° |
 )的直线的倾斜角是( )
)的直线的倾斜角是( ) )的直线的斜率是( )
)的直线的斜率是( )