题目内容
设 为抛物线
为抛物线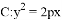 的焦点,过
的焦点,过 且倾斜角为60°的直线交曲线
且倾斜角为60°的直线交曲线 于
于 两点(
两点( 点在第一象限,
点在第一象限, 点在第四象限),
点在第四象限), 为坐标原点,过
为坐标原点,过 作
作 的准线的垂线,垂足为
的准线的垂线,垂足为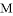 ,则
,则 与
与 的比为( )
的比为( )
A.  B. 2 C. 3 D. 4
B. 2 C. 3 D. 4
练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
题目内容
设 为抛物线
为抛物线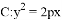 的焦点,过
的焦点,过 且倾斜角为60°的直线交曲线
且倾斜角为60°的直线交曲线 于
于 两点(
两点( 点在第一象限,
点在第一象限, 点在第四象限),
点在第四象限), 为坐标原点,过
为坐标原点,过 作
作 的准线的垂线,垂足为
的准线的垂线,垂足为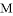 ,则
,则 与
与 的比为( )
的比为( )
A.  B. 2 C. 3 D. 4
B. 2 C. 3 D. 4
 寒假学与练系列答案
寒假学与练系列答案