题目内容
（本题满分12分）对于函数
，若存在
，使得
成立，称
为不动点，已知函数
当
时，求函数
不动点；
若对任意的实数
，函数恒有两个相异的不动点，求a的取值范围；
在（2）的条件下，若图象上A，B两点的横坐标是函数不动点，且
两点关于直线
对称，求b的最小值.
解：（1）当
时，
，令
，解之得
所以
的不动点是-1，3
（2）
恒有两个不动点，所以
，
即
恒有两个相异实根，得
恒成立。于是
解得
所以a的取值范围为
（3）由题意，A、B两点应在直线
上，
设A
，因为AB关于直线
对称，所以
设AB中点为M
，因为
是方程的两个根。
所以
于是点M在直线
上，代入得
即
当且仅当
即
时取等号。
故
的最小值为
练习册系列答案
相关题目
)：（本题满分12分）
对某校高二年级学生参加社会实践活动次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社会实践活动的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如下：
|
分组 |
频数 |
频率 |
|
|
10 |
0.25 |
|
|
26 |
n |
|
|
m |
P |
|
|
1 |
0.025 |
|
合计 |
M |
1 |
（Ⅰ）求出表中M，P及图中
的值；
（Ⅱ）在所取样本中，从参加社会实践活动的次数不少于20次的学生中任选2人，求恰有一人参加社会实践活动次数在区间
内的概率．
是抛物线
上的点，过焦点F的直线FAn交抛物线另一点
。
并
为抛物线上分别为
与
为切点的两条切线的交点，求证
)：(本题满分12分)
网络对现代人的生活影响较大, 尤其对青少年. 为了了解网络对中学生学习成绩的影响, 某地区教育局从辖区高中生中随机抽取了1000人进行调查, 具体数据如下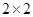
列联表所示．
|
|
经常上网 |
不经常上网 |
合计 |
|
不及格 |
80 |
a |
200 |
|
及格 |
b |
680 |
c |
|
合计 |
200 |
d |
1000 |
(1)求a,b,c,d；
(2)利用独立性检验判断, 有多大把握认为上网对高中生的学习成绩有关．