题目内容
(本题满分12分)
对某校高二年级学生参加社会实践活动次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社会实践活动的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
|
分组 |
频数 |
频率 |
|
|
10 |
0.25 |
|
|
26 |
n |
|
|
m |
P |
|
|
1 |
0.025 |
|
合计 |
M |
1 |

(Ⅰ)求出表中M,P及图中 的值;
的值;
(Ⅱ)在所取样本中,从参加社会实践活动的次数不少于20次的学生中任选2人,求恰有一人参加社会实践活动次数在区间 内的概率.
内的概率.
【答案】
(Ⅰ)M=40.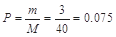 .
.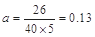 .(Ⅱ)
P=
.(Ⅱ)
P=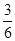 =
= .
.
【解析】
试题分析:(Ⅰ)由分组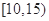 内的频数是10,频率是0.25知,
内的频数是10,频率是0.25知,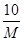 =0.25,
=0.25,
所以M=40. ……2分
因为频数之和为40,所以10+26+m+1=40,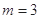 .
.
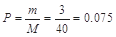 .……4分
.……4分
因为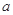 是对应分组
是对应分组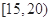 的频率与组距的商,所以
的频率与组距的商,所以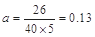 .
……6分
.
……6分
(Ⅱ)这个样本中,参加社会实践活动次数不少于20次的学生共有m+1=4人,
设在区间[20,25)内的人为a1,a2,a3,在区间[20,25)内的人为b,则任选2人共有(a1,a2),(a1,a3),(a2,a3),(a1,b),(a2,b),(a3,b)共6种情况.……9分
恰有一人参加社会实践活动次数在区间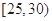 内的情况有(a1,b),(a2,b),(a3,b)共3种情况.
内的情况有(a1,b),(a2,b),(a3,b)共3种情况.
所以,所求的概率为P=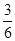 =
= .……12分
.……12分
考点:本题主要考查抽样方法,频率的概念及计算,古典概型概率的计算。
点评:典型题,统计中的抽样方法,频率直方图,概率计算及分布列问题,是高考必考内容及题型。古典概型概率的计算问题,关键是明确基本事件数,往往借助于“树图法”,做到不重不漏。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目



 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面