题目内容
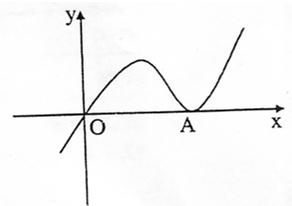 函数y=ax3-x2+cx(a≠0)的图象如图所示,它与x轴仅有两个公共点O(0,0)与A(xA,0)(xA>0);(1)用反证法证明常数c≠0;(2)如果xA=
函数y=ax3-x2+cx(a≠0)的图象如图所示,它与x轴仅有两个公共点O(0,0)与A(xA,0)(xA>0);(1)用反证法证明常数c≠0;(2)如果xA=| 1 | 2 |
分析:(1)根据反证明法的证明方法,先假设c=0,则y=ax3-x2=x2(ax-1),这与图象所给的矛盾,从而得出c≠0;
(2)由(1)知c≠0,得出y=x(ax2-x+c),图象与x轴仅有两个公共点,得出方程ax2-x+c=0(a≠0)有二等根
.
由韦达定理列出关于a,c.的方程,解之即可.
(2)由(1)知c≠0,得出y=x(ax2-x+c),图象与x轴仅有两个公共点,得出方程ax2-x+c=0(a≠0)有二等根
| 1 |
| 2 |
由韦达定理列出关于a,c.的方程,解之即可.
解答:解:(1)假设c=0,则y=ax3-x2=x2(ax-1);
∴xA=
>0,当x<xA时,f(x)<0这与图象所给的:
当0<x<xA时,f(x)>0矛盾,∴c≠0
(2)由(1)知c≠0,∴y=x(ax2-x+c)
∵图象与x轴仅有两个公共点,
∴方程ax2-x+c=0(a≠0)有二等根
.
由韦达定理
,∴
,∴y=x3-x2+
x
∴xA=
| 1 |
| a |
当0<x<xA时,f(x)>0矛盾,∴c≠0
(2)由(1)知c≠0,∴y=x(ax2-x+c)
∵图象与x轴仅有两个公共点,
∴方程ax2-x+c=0(a≠0)有二等根
| 1 |
| 2 |
由韦达定理
|
|
| 1 |
| 4 |
点评:本小题主要考查函数的图象与图象变化、函数解析式的求解及常用方法等基础知识,考查运算求解能力,考查数形结合思想,属于基础题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
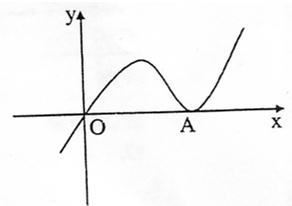 函数y=ax3-x2+cx(a≠0)的图象如图所示,它与x轴仅有两个公共点O(0,0)与A(xA,0)(xA>0);(1)用反证法证明常数c≠0;(2)如果
函数y=ax3-x2+cx(a≠0)的图象如图所示,它与x轴仅有两个公共点O(0,0)与A(xA,0)(xA>0);(1)用反证法证明常数c≠0;(2)如果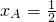 ,求函数的解析式.
,求函数的解析式.