题目内容
有下列命题中假命题的序号是
①x=0是函数y=x3的极值点;
②三次函数f(x)=ax3+bx2+cx+d有极值点的充要条件是b2-3ac>0;
③奇函数f(x)=mx3+(m-1)x2+48(m-2)x+n在区间(-4,4)上单调递减.
④若双曲线的渐近线方程为y=±
x,则其离心率为2.
①④
①④
①x=0是函数y=x3的极值点;
②三次函数f(x)=ax3+bx2+cx+d有极值点的充要条件是b2-3ac>0;
③奇函数f(x)=mx3+(m-1)x2+48(m-2)x+n在区间(-4,4)上单调递减.
④若双曲线的渐近线方程为y=±
| 3 |
分析:①用极值点的定义的来判断;②通过导数有不等根来判断;③用f′(x)<0,x∈(-4,4)恒成立来判断;④若双曲线的渐近线方程为y=±
x,则
=
或
=
,可求离心率.
| 3 |
| b |
| a |
| 3 |
| a |
| b |
| 3 |
解答:解:①取导函数,可得y′=3x2≥0,∴函数在R上单调递增,∴函数无极值点,故是假命题;
①求导函数,可得f′(x)=3ax2+2bx+c,∴三次函数f(x)=ax3+bx2+cx+d有极值点的充要条件是导数有不等根,即4b2-12ac>0,即b2-3ac>0,故是真命题;
③∵函数是奇函数,∴f(-x)=f(x),求得m=1,n=0,∴f′(x)=3x2-48<0x∈(-4,4)恒成立
∴f(x)=mx3+(m-1)x2+48(m-2)x+n在区间(-4,4)上是单调减函数,故是真命题;
④若双曲线的渐近线方程为y=±
x,则
=
或
=
,∴其离心率为2或
,故是假命题.
故答案为①④
①求导函数,可得f′(x)=3ax2+2bx+c,∴三次函数f(x)=ax3+bx2+cx+d有极值点的充要条件是导数有不等根,即4b2-12ac>0,即b2-3ac>0,故是真命题;
③∵函数是奇函数,∴f(-x)=f(x),求得m=1,n=0,∴f′(x)=3x2-48<0x∈(-4,4)恒成立
∴f(x)=mx3+(m-1)x2+48(m-2)x+n在区间(-4,4)上是单调减函数,故是真命题;
④若双曲线的渐近线方程为y=±
| 3 |
| b |
| a |
| 3 |
| a |
| b |
| 3 |
2
| ||
| 3 |
故答案为①④
点评:本题考查函数的极值与单调性,考查双曲线的几何性质,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
相关题目
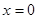 是函数
是函数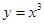 的极值点;
的极值点;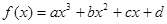 有极值点的充要条件是
有极值点的充要条件是
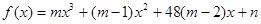 在区间
在区间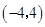 上单调递减.
上单调递减.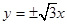 ,则其离心率为2.
,则其离心率为2.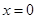 是函数
是函数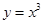 的极值点;
的极值点;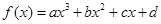 有极值点的充要条件是
有极值点的充要条件是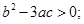
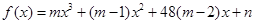 在区间
在区间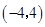 上单调递减.
上单调递减.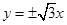 ,则其离心率为2.
,则其离心率为2.