题目内容
计算:(1)a
(a、b是不为1的正数，c>0)；
(2)lg5·lg8000+(lg2
)2－lg6+lg0.06；
(3)5
·(
)
；
(4)(log2125+log425+log85)·(log1258+log254+log52).
解:(1)∵logab·logbc==logac,∴a=a=c.
(2)原式=lg5(3+lg8)+(lg2)2－lg6+lg6－2=(1－lg2)·3(1+lg2)+3lg22－2=3(1－lg22)+3lg22－2=1.
(3)设y=5·(
)
,则lgy=lg5
+lg(
)
=lg30·lg5+lg0.5·lg
=(1+lg3)lg5+lg2lg3=lg5+lg3(lg5+lg2)=lg5+lg3=lg15,∴y=15,即5
·(
)
=15.
(4)原式=(3log25+log25+
log25)(log52+log52+log52)=
log25·3log52=13.
练习册系列答案
相关题目
如图，这是一个计算机装置示意图，A、B是数据入口处，C是计算机结果的出口，计算过程是由A、B分别输入自然数m和n，经过计算后，得自然数k，由C输出．即：f（m，n）=k，此种计算装置完成计算，满足以下三个性质：①若A、B分别输入1，则输出结果为1，即f（1，1）=1；②若A输入自然数m，B输入自然数由n变为n+1，则输出结果比原来增大2，即f（m，n+1）=f（m，n）+2；③若B输入1，A输入自然数由m变为m+1，则输出结果是原来的2倍，即f（m+1，1）=2f（m，1）．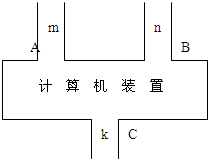
如图，这是一个计算机装置示意图，A、B是数据入口处，C是计算机结果的出口，计算过程是由A、B分别输入自然数m和n，经过计算后，得自然数k，由C输出．即：f（m，n）=k，此种计算装置完成计算，满足以下三个性质：①若A、B分别输入1，则输出结果为1，即f（1，1）=1；②若A输入自然数m，B输入自然数由n变为n+1，则输出结果比原来增大2，即f（m，n+1）=f（m，n）+2；③若B输入1，A输入自然数由m变为m+1，则输出结果是原来的2倍，即f（m+1，1）=2f（m，1）．