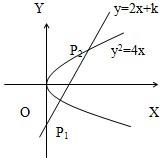
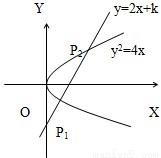
题目内容
(1)设抛物线y2=4x截直线y=2x+k所得的弦长为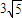 ,求k的值.
,求k的值.(2)以本题(1)得到的弦为底边,以x轴上的点P为顶点做成三角形,当这三角形的面积为9时,求P的坐标.
【答案】分析:(1)设出交点坐标,联立直线和抛物线的方程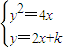 ,整理,由韦达定理,算出(x1-x2)2,(y1-y2)2,再有两点间距离公式计算出弦长.求出k.
,整理,由韦达定理,算出(x1-x2)2,(y1-y2)2,再有两点间距离公式计算出弦长.求出k.
(2)设出P点坐标,由点p到直线的距离求出三角形的高,再由面积公式代入求解,即得.
解答:解:(1)设直线与抛物线的交点为P1(x1,y1),P2(x2,y2).
解方程组: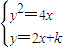 ,得(2x+k)2=4x,
,得(2x+k)2=4x,
即4x2+4(k-1)x+k2=0,
故有x1+x2=1-k,x1x2= .
.
∴(x1-x2)2=(x1+x2)2-4x1x2
=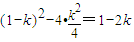 .
.
又因P1,P2在直线y=2x+k上,故
(y1-y2)2=4(x1-x2)2=4(1-2k).
根据题设条件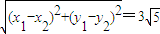 ,
,
即(1-2k)+4(1-2k)=45,解得:k=-4.
(2)设x轴上一点P的坐标为(a,0)又点P到直线P1P2的距离为h,则有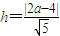 .
.
依题意得△PP1P2的面积关系: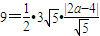 ,即6=|2a-4|,
,即6=|2a-4|,
∴a=5,a=-1.
点评:“设而不求”仍是圆锥曲线问题的常用方法,在第一题的处理中,也可直接用弦长公式lAB= |x1-x2|.
|x1-x2|.
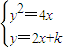 ,整理,由韦达定理,算出(x1-x2)2,(y1-y2)2,再有两点间距离公式计算出弦长.求出k.
,整理,由韦达定理,算出(x1-x2)2,(y1-y2)2,再有两点间距离公式计算出弦长.求出k.(2)设出P点坐标,由点p到直线的距离求出三角形的高,再由面积公式代入求解,即得.
解答:解:(1)设直线与抛物线的交点为P1(x1,y1),P2(x2,y2).
解方程组:
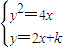 ,得(2x+k)2=4x,
,得(2x+k)2=4x,即4x2+4(k-1)x+k2=0,
故有x1+x2=1-k,x1x2=
 .
.∴(x1-x2)2=(x1+x2)2-4x1x2
=
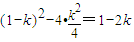 .
.又因P1,P2在直线y=2x+k上,故
(y1-y2)2=4(x1-x2)2=4(1-2k).
根据题设条件
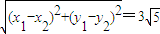 ,
,即(1-2k)+4(1-2k)=45,解得:k=-4.
(2)设x轴上一点P的坐标为(a,0)又点P到直线P1P2的距离为h,则有
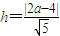 .
.依题意得△PP1P2的面积关系:
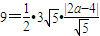 ,即6=|2a-4|,
,即6=|2a-4|,∴a=5,a=-1.
点评:“设而不求”仍是圆锥曲线问题的常用方法,在第一题的处理中,也可直接用弦长公式lAB=
 |x1-x2|.
|x1-x2|. 
练习册系列答案
相关题目