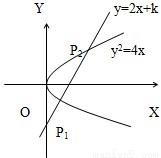
题目内容
设抛物线y2=4x截直线y=2x+m所得的弦AB长为3
.
(1)求m的值;
(2)以弦AB为底边,以x轴上的点P为顶点组成的三角形的面积为39时,求点P的坐标.
| 5 |
(1)求m的值;
(2)以弦AB为底边,以x轴上的点P为顶点组成的三角形的面积为39时,求点P的坐标.
分析:(1)联立方程
可得,4x2+4(m-1)x+m2=0由△>0有 16(m-1)2-16m2>0得m<
由AB=3
=
可求m
(2)设P(x0,0),先求点P(x0,0)到AB:2x-y-4=0距离 d =
,再根据
|AB|d=39,可求P得坐标
|
| 1 |
| 2 |
由AB=3
| 5 |
| (1+k2)[(x1+x2)2-4x1x2] |
(2)设P(x0,0),先求点P(x0,0)到AB:2x-y-4=0距离 d =
| |2x0-4| | ||
|
| 1 |
| 2 |
解答:解:(1)
∴4x2+4(m-1)x+m2=0
由△>0有 16(m-1)2-16m2>0
解得m<
设A(x1,y1)B(x2,y2),则x1+x2=1-mx1x2=
,
∵AB=3
=
解得 m=-4 适合m<
∴m=-4
(2)设P(x0,0)则点P(x0,0)到AB:2x-y-4=0距离 d =
依题意
|AB|d=39,∴
•3
•
=39,∴x0=15或x0=-11
∴P(15,0)或P(-11,0)
|
由△>0有 16(m-1)2-16m2>0
解得m<
| 1 |
| 2 |
设A(x1,y1)B(x2,y2),则x1+x2=1-mx1x2=
| m2 |
| 4 |
∵AB=3
| 5 |
| (1+k2)[(x1+x2)2-4x1x2] |
解得 m=-4 适合m<
| 1 |
| 2 |
∴m=-4
(2)设P(x0,0)则点P(x0,0)到AB:2x-y-4=0距离 d =
| |2x0-4| | ||
|
依题意
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| |2x0-4| | ||
|
∴P(15,0)或P(-11,0)
点评:本题主要考查了直线与抛物线相交求解弦长,关键是根据方程的根与系数的关系表示由AB=
,这是圆锥曲线的考查的热点之一.
| (1+k2)[(x1+x2)2-4x1x2] |

练习册系列答案
相关题目
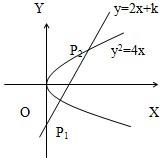
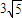 ,求k的值.
,求k的值.