题目内容
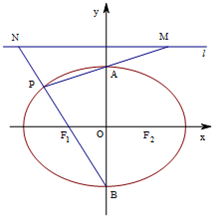 如图,焦点在x轴上的椭圆的离心率为
如图,焦点在x轴上的椭圆的离心率为
| ||
| 2 |
(1)求MN的最小值;
(2)证明以MN为直径的圆恒过定点,并求出定点坐标.
分析:(1)利用椭圆离心率的意义和a、b、c的关系即可求出椭圆的方程;先设出点M、N的坐标,可写出直线MA、MB的方程,联立即可得出点P的坐标,再代入椭圆方程即可得出m、n的关系,进而求出|MN|最小值;
(2)先写出圆的方程,再利用(1)结论即可求出.
(2)先写出圆的方程,再利用(1)结论即可求出.
解答:解:(1)设椭圆的方程为
+
=1(a>b>0),由题意可得
,解得
,
∴椭圆的方程为
+y2=1.
设点M(m,2),N(n,2)不妨设m>0,n<0.
则直线MA的方程为:y=
x+1;直线NB的方程为y=
x-1.
联立
解得
,即点P(
,
).
代入椭圆的方程得
+
=1,化为mn=-12.
∴|MN|=m-n=m+
≥2
=4
,当且仅当m=2
时取等号,即|MN|的最小值为4
.
(3)由(1)可知:设(M(m,2),N(n,2)),则mn=-12.
∴以MN为直径的圆的方程为(x-
)2+(y-2)2=(
)2.
令x=0,则方程化为(y-2)2=12,解得y=2±2
.
∴以MN为直径的圆恒过定点(0,2±2
).
| x2 |
| a2 |
| y2 |
| b2 |
|
|
∴椭圆的方程为
| x2 |
| 4 |
设点M(m,2),N(n,2)不妨设m>0,n<0.
则直线MA的方程为:y=
| 1 |
| m |
| 3 |
| n |
联立
|
|
| 2mn |
| 3m-n |
| 3m+n |
| 3m-n |
代入椭圆的方程得
| m2n2 |
| (3m-n)2 |
| (3m+n)2 |
| (3m-n)2 |
∴|MN|=m-n=m+
| 12 |
| m |
m×
|
| 3 |
| 3 |
| 3 |
(3)由(1)可知:设(M(m,2),N(n,2)),则mn=-12.
∴以MN为直径的圆的方程为(x-
| m+n |
| 2 |
| m-n |
| 2 |
令x=0,则方程化为(y-2)2=12,解得y=2±2
| 3 |
∴以MN为直径的圆恒过定点(0,2±2
| 3 |
点评:熟练掌握椭圆的定义与性质、直线相交问题的解法、代点法、圆的方程及恒过定点问题的解法是解题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
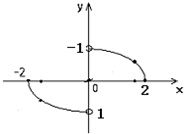 如图,函数y=f(x)的图象是中心在原点,焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )
如图,函数y=f(x)的图象是中心在原点,焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )A、{
| ||||||||
B、{x|-2≤x<
| ||||||||
C、{x|-
| ||||||||
D、{x|-
|
 如图,已知焦点在x轴上的椭圆
如图,已知焦点在x轴上的椭圆 如图,在直角坐标系中,中心在原点,焦点在x轴上的椭圆G的离心率为
如图,在直角坐标系中,中心在原点,焦点在x轴上的椭圆G的离心率为 如图,已知中心在原点0、焦点在x轴上的椭圆T过点M(2,1),离心率为
如图,已知中心在原点0、焦点在x轴上的椭圆T过点M(2,1),离心率为