题目内容
已知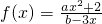 是定义在(-∞,0)∪(0,+∞)上的奇函数,
是定义在(-∞,0)∪(0,+∞)上的奇函数,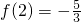 .
.
(1)求a,b的值;
(2)请用函数单调性的定义说明:f(x)在区间(1,+∞)上的单调性;
(3)求f(x)的值域.
解:(1)由f(-x)=-f(x)得:b=0,由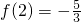 得a=2…..
得a=2…..
(2)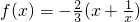 在(1,+∞)上为减函数.
在(1,+∞)上为减函数.
证明:任取1<x1<x2,则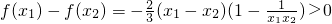 ,
,
所以f(x)在(1,+∞)上为减函数…
(3)同理,f(x)在(0,1)递增∴x>0时,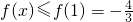 ,
,
又f(x)为奇函数,∴x<0时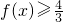 ,
,
综上所述,f(x)的值域为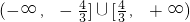 …
…
分析:(1)由f(-x)=-f(x)可求b,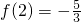 ,可求a;
,可求a;
(2)利用函数单调性的定义任取1<x1<x2,作差f(x1)-f(x2),判断符号;
(3)利用函数单调性与奇偶性即可求得f(x)的值域.
点评:本题考查函数奇偶性与单调性,重点考查学生理解函数奇偶性单调性及灵活应用之求值域,解决的方法是特值法与函数单调性的定义法,属于中档题.
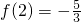 得a=2…..
得a=2…..(2)
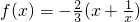 在(1,+∞)上为减函数.
在(1,+∞)上为减函数.证明:任取1<x1<x2,则
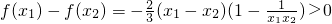 ,
,所以f(x)在(1,+∞)上为减函数…
(3)同理,f(x)在(0,1)递增∴x>0时,
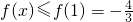 ,
,又f(x)为奇函数,∴x<0时
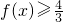 ,
,综上所述,f(x)的值域为
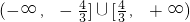 …
…分析:(1)由f(-x)=-f(x)可求b,
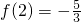 ,可求a;
,可求a;(2)利用函数单调性的定义任取1<x1<x2,作差f(x1)-f(x2),判断符号;
(3)利用函数单调性与奇偶性即可求得f(x)的值域.
点评:本题考查函数奇偶性与单调性,重点考查学生理解函数奇偶性单调性及灵活应用之求值域,解决的方法是特值法与函数单调性的定义法,属于中档题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
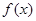 是定义在R上的偶函数,对任意
是定义在R上的偶函数,对任意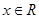 ,都有
,都有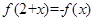 ,且当
,且当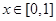 时在
时在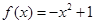 ,若
,若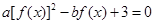 在
在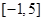 上有5个根
上有5个根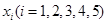 ,则
,则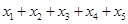 的值为( )
的值为( )