题目内容
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.A.[选修4-1:几何证明选讲]
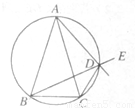
已知△ABC中,AB=AC,D是△ABC外接圆劣弧AC上的点(不与点A,C重合),延长BD至点E.
求证:AD的延长线平分∠CDE
B.[选修4-2:矩阵与变换]
已知矩阵
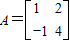
(1)求A的逆矩阵A-1;
(2)求A的特征值和特征向量.
C.[选修4-4:坐标系与参数方程]
已知曲线C的极坐标方程为ρ=4sinθ,以极点为原点,极轴为x轴的非负半轴建立平面直角坐标系,直线l的参数方程为
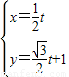 (t为参数),求直线l被曲线C截得的线段长度.
(t为参数),求直线l被曲线C截得的线段长度.D.[选修4-5,不等式选讲](本小题满分10分)
设a,b,c均为正实数,求证:
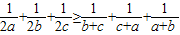 .
.
【答案】分析:A.要证AD 的延长线平分∠CDE,即证∠EDF=∠CDF,根据A,B,C,D 四点共圆,可得∠ABC=∠CDF,AB=AC可得∠ABC=∠ACB,从而得解.
B.(1)根据所给的矩阵求这个矩阵的逆矩阵,可以首先求出ad-bc的值,再代入逆矩阵的公式,求出结果.
(2)先根据特征值的定义列出特征多项式,令f(λ)=0解方程可得特征值,再由特征值列出方程组即可解得相应的特征向量.
C.曲线C为:x2+y2-4y=0,圆心(0,2),半径为2,由此能求出直线被曲线C载得的线段长度.
D.对左边变形 (
( +
+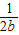 )+
)+ (
(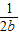 +
+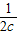 )+
)+ (
(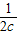 +
+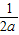 )后两项应用基本不等式,得到三个不等式后相加即得.
)后两项应用基本不等式,得到三个不等式后相加即得.
解答:解:A:设F为AD 延长线上一点,
∵A,B,C,D 四点共圆,∴∠ABC=∠CDF,
∵AB=AC,∴∠ABC=∠ACB,
∵∠ADB=∠ACB,∴∠ADB=∠CDF,
∵对顶角∠EDF=∠ADB,∴∠EDF=∠CDF,
故AD的延长线平分∠CDE.
B:解:(1)ad-bc=4+2=6,
A-1= =
=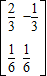 ,
,
∴A-1=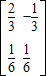 .
.
(2)矩阵A的特征多项式为f(λ)=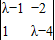 =λ2-5λ+6,
=λ2-5λ+6,
令f(λ)=0,得λ1=2,λ2=3,
当λ1=2时,得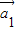 =
= ,当λ2=3时,得
,当λ2=3时,得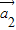 =
= .
.
所以矩阵A属于特征值2的一个特征向量为 ,
,
矩阵M属于特征值3的一个特征向量为 .
.
C:曲线C为:x2+y2-4y=0,圆心(0,2),半径为2,
直线l为: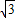 x-y+1=0,圆心到直线的距离为:d=
x-y+1=0,圆心到直线的距离为:d=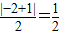
直线被曲线C载得的线段长度为:2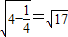 .
.
D:证明:∵a、b、c均为实数,
∴ (
( +
+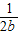 )≥
)≥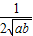 ≥
≥ ,当a=b时等号成立;
,当a=b时等号成立;
 (
(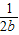 +
+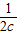 )≥
)≥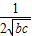 ≥
≥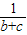 ,
,
当b=c时等号成立;
 (
(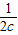 +
+ )≥
)≥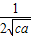 ≥
≥ .
.
三个不等式相加即得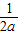 +
+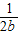 +
+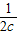 ≥
≥ +
+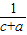 +
+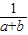 ,
,
当且仅当a=b=c时等号成立.
点评:A考查直线与圆的位置关系,B考查逆矩阵的求法和矩阵的特征值和特征向量的求法,C考查极坐标标方程和参数方程的应用,D考查不等式的证明.都是基础题,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.
B.(1)根据所给的矩阵求这个矩阵的逆矩阵,可以首先求出ad-bc的值,再代入逆矩阵的公式,求出结果.
(2)先根据特征值的定义列出特征多项式,令f(λ)=0解方程可得特征值,再由特征值列出方程组即可解得相应的特征向量.
C.曲线C为:x2+y2-4y=0,圆心(0,2),半径为2,由此能求出直线被曲线C载得的线段长度.
D.对左边变形
 (
( +
+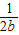 )+
)+ (
(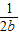 +
+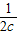 )+
)+ (
(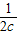 +
+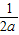 )后两项应用基本不等式,得到三个不等式后相加即得.
)后两项应用基本不等式,得到三个不等式后相加即得.解答:解:A:设F为AD 延长线上一点,
∵A,B,C,D 四点共圆,∴∠ABC=∠CDF,
∵AB=AC,∴∠ABC=∠ACB,
∵∠ADB=∠ACB,∴∠ADB=∠CDF,
∵对顶角∠EDF=∠ADB,∴∠EDF=∠CDF,
故AD的延长线平分∠CDE.
B:解:(1)ad-bc=4+2=6,
A-1=
 =
= ,
,∴A-1=
 .
.(2)矩阵A的特征多项式为f(λ)=
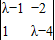 =λ2-5λ+6,
=λ2-5λ+6,令f(λ)=0,得λ1=2,λ2=3,
当λ1=2时,得
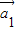 =
= ,当λ2=3时,得
,当λ2=3时,得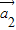 =
= .
.所以矩阵A属于特征值2的一个特征向量为
 ,
,矩阵M属于特征值3的一个特征向量为
 .
.C:曲线C为:x2+y2-4y=0,圆心(0,2),半径为2,
直线l为:
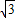 x-y+1=0,圆心到直线的距离为:d=
x-y+1=0,圆心到直线的距离为:d=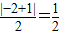
直线被曲线C载得的线段长度为:2
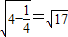 .
.D:证明:∵a、b、c均为实数,
∴
 (
( +
+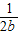 )≥
)≥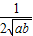 ≥
≥ ,当a=b时等号成立;
,当a=b时等号成立; (
(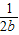 +
+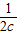 )≥
)≥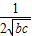 ≥
≥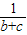 ,
,当b=c时等号成立;
 (
(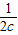 +
+ )≥
)≥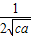 ≥
≥ .
.三个不等式相加即得
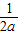 +
+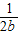 +
+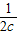 ≥
≥ +
+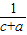 +
+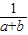 ,
,当且仅当a=b=c时等号成立.
点评:A考查直线与圆的位置关系,B考查逆矩阵的求法和矩阵的特征值和特征向量的求法,C考查极坐标标方程和参数方程的应用,D考查不等式的证明.都是基础题,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤. (2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
(2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. 与圆
与圆 内切于点
内切于点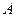 ,其半径分别为
,其半径分别为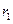 与
与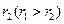 ,
,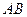 交圆
交圆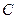 (
(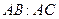 为定值。
为定值。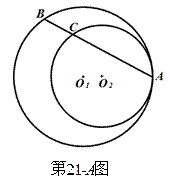
 如图,圆
如图,圆 与圆
与圆 内切于点
内切于点 ,其半径分别为
,其半径分别为 与
与 ,
, 交圆
交圆 (
( 为定值。
为定值。 ,向量
,向量 ,求向量
,求向量 ,使得
,使得 .
. 中,求过椭圆
中,求过椭圆 (
( 为参数)的右焦点且与直线
为参数)的右焦点且与直线 (
( 为参数)平行的直线的普通方程。
为参数)平行的直线的普通方程。