Question

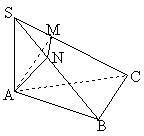
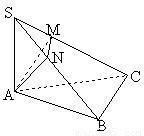
225、如图，在空间四面体S-ABC中，已知∠ABC=90°，SA⊥平面ABC，AN⊥SB，AM⊥SC，证明：SC⊥平面AMN．

Answer 1

分析：由结论联想判定定理，要证明SC⊥平面AMN，需证明SC垂直于平面AMN中的两条相交直线．已知AM⊥SC，尚缺条件SC⊥AN．于是考虑从其它条件所具备的性质中去寻找．

解答：证明：∵SA⊥平面ABC，而AB为SB在平面ABC内的射影，
又由∠ABC=90°，知BC⊥AB，由三垂线定理，BC⊥SB，∴BC⊥平面SAB，
∵AN?平面SAB，∴BC⊥AN，∴AN⊥平面SBC，∴SC⊥AN，
∵AM⊥SC，∴SC⊥平面AMN．

点评：本题在运用判定定理证明线面垂直（SC⊥平面AMN）时，将问题化为利用定义证明线线垂直（SC⊥AN）；而证明此线线垂直时，又转化为利用判定定理证明线面垂直（AN⊥平面SBC），又利用定义转化为证明BC⊥AN．