Question

若椭圆中心为坐标原点，焦点在轴上，过点（1，）作圆的切线，切点分别为，直线恰好经过椭圆的右焦点和上顶点，则椭圆方程是                    .

Answer 1

【答案】

【解析】设过点（1，）的圆的切线为l：。

①直线l与x轴垂直时，k不存在，直线方程为x=1，恰好与圆相切于点A（1，0）；②当直线l与x轴不垂直时，原点到直线l的距离为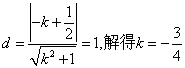：，此时直线l的方程为 ，l切圆x2+y2=1相切于点，因此，直线AB斜率为，直线AB方程为，∴直线AB交x轴交于点A（1，0），交y轴于点C（0，2）．所以椭圆的右焦点为（0，1），上顶点为（0，2），∴c=1，b=2，可得，所以椭圆方程为。