题目内容
（本小题满分12分）
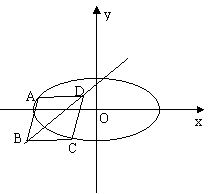
已知菱形
的顶点
在椭圆
上，对角线
所在直线的斜率为1．
（1）当直线过点
时，求直线
的方程；
（2）当
时，求菱形面积的最大值．
解：（1）由题意得直线
的方程为
．因为四边形
为菱形，所以
．
于是可设直线
的方程为
．
由
得
．
因为
在椭圆上，所以
，解得
．
设两点坐标分别为
，则
，
，
，
．所以
．所以的中点坐标为
．
由四边形为菱形可知，点
在直线上， 所以
，
解得
．所以直线的方程为
，即
．
（2）因为四边形为菱形，且
，所以
．
所以菱形的面积
．
由（1）可得
，所以
．
所以当
时，菱形的面积取得最大值
．
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
