题目内容
给出下列命题:①函数
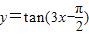 的最小正周期是
的最小正周期是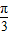
②角α终边上一点P(-3a,4a),且a≠0,那么
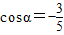
③函数
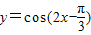 的图象的一个对称中心是
的图象的一个对称中心是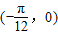
④已知向量
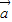 =(1,2),
=(1,2),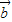 =(1,0),
=(1,0),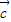 =(3,4).若λ为实数,且(
=(3,4).若λ为实数,且(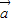 +λ
+λ )∥
)∥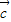 ,则λ=2
,则λ=2⑤设f(x)是定义在R上的奇函数,当x≤0时,f(x)=2x2-x,则f(1)=-3
其中正确的个数有( )
A.1个
B.2个
C.3个
D.4个
【答案】分析:根据正切函数的最小正周期是π,判断①是否正确;
利用三角函数定义,r=|5a|,用定义验证②是否正确;
令x=-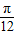 ,求2x-
,求2x- ,验证③是否正确;
,验证③是否正确;
利用向量的线性运算与共线的坐标表示求解,判断④的正确性;
利用奇函数的性质f(1)与f(-1)的关系求解即可.
解答:解:根据正切函数的最小正周期,①√;
∵根据三角函数定义 cosα= ,当a<0时cosα=
,当a<0时cosα= ,∴②×;
,∴②×;
∵x=-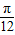 ⇒2x-
⇒2x-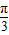 =-
=-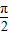 ,∴③√;
,∴③√;
∵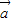 +λ
+λ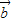 =(1+λ,2),∵(
=(1+λ,2),∵( +λ
+λ )∥
)∥ ⇒λ=
⇒λ= ,∴④×;
,∴④×;
∵f(1)=-f(-1)=-(2+1)=-3,∴⑤√;
故选C
点评:本题考查了三角函数的定义,平面向量共线的坐标表示,三角函数的对称中心、周期问题,以及函数奇偶性的应用. =(x1,y1),
=(x1,y1),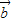 =(x2,y2);
=(x2,y2);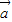 ∥
∥ ?x1y2-x2y1=0.
?x1y2-x2y1=0.
利用三角函数定义,r=|5a|,用定义验证②是否正确;
令x=-
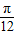 ,求2x-
,求2x- ,验证③是否正确;
,验证③是否正确;利用向量的线性运算与共线的坐标表示求解,判断④的正确性;
利用奇函数的性质f(1)与f(-1)的关系求解即可.
解答:解:根据正切函数的最小正周期,①√;
∵根据三角函数定义 cosα=
 ,当a<0时cosα=
,当a<0时cosα= ,∴②×;
,∴②×;∵x=-
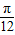 ⇒2x-
⇒2x-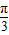 =-
=-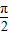 ,∴③√;
,∴③√;∵
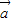 +λ
+λ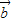 =(1+λ,2),∵(
=(1+λ,2),∵( +λ
+λ )∥
)∥ ⇒λ=
⇒λ= ,∴④×;
,∴④×;∵f(1)=-f(-1)=-(2+1)=-3,∴⑤√;
故选C
点评:本题考查了三角函数的定义,平面向量共线的坐标表示,三角函数的对称中心、周期问题,以及函数奇偶性的应用.
 =(x1,y1),
=(x1,y1),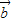 =(x2,y2);
=(x2,y2);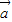 ∥
∥ ?x1y2-x2y1=0.
?x1y2-x2y1=0. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目