题目内容
(08年山西大学附中五模理) 如图,![]() ,
,![]() .
.![]() 垂直于
垂直于![]() 于
于![]() ,
,![]() 垂直于
垂直于![]() 于
于![]() .
.
![]() .
.
(Ⅰ)求证:![]()
![]() ;
;
(Ⅱ)求![]() 与平面
与平面![]() 所成的角;
所成的角;
(Ⅲ)![]() 为线段
为线段![]() 上的点,试确定点
上的点,试确定点![]() 的位置,使得
的位置,使得![]() .
.

解析:解法一:(1)证明:因为![]() ,
,
所以![]() ,又
,又![]() ,
,
所以![]() ,则
,则![]() ,
,
又![]() ,所以
,所以![]() ,
,
得![]() 又
又![]() ,所以
,所以![]() .
.
(2)在平面PBC上,过点B作BF平行于PC交ED延长线于点F,
连结AF,因为![]() ,所以
,所以![]() ,
,
所以![]() 为直线AB和平面ADE所成的角.
为直线AB和平面ADE所成的角.
在三角形PBC中, PD=![]() ,则BD=
,则BD=![]() ,得BF=
,得BF=![]() .
.
在![]() 中,
中,![]() ,线AB与面ADE所成角为
,线AB与面ADE所成角为![]() .
.
(3)过点B作BM∥DE交PC于点M,过M作M![]() ∥AE交AC于点Q,则平面BMQ∥平面ADE,得B
∥AE交AC于点Q,则平面BMQ∥平面ADE,得B![]() ∥平面ADE,点Q即为所求的点.
∥平面ADE,点Q即为所求的点.
下面确定点Q的位置。因为BM∥DE,则![]() ,可得点M为CE的中点,因为MQ∥AE,所以点Q为AC中点.
,可得点M为CE的中点,因为MQ∥AE,所以点Q为AC中点.
解法二:(1)同解法一
(2)过点B作BZ∥AP,则BZ![]() 平面ABC,如图所示,分别以BA,BC,BZ所在直线为x轴,y轴,z轴建立空间直角坐标系。则A(1,0,0),C(0,1,0), P(1,0,
平面ABC,如图所示,分别以BA,BC,BZ所在直线为x轴,y轴,z轴建立空间直角坐标系。则A(1,0,0),C(0,1,0), P(1,0,![]() )
)
因为![]() .
.
设向量![]() 所成的角为
所成的角为![]() ,则
,则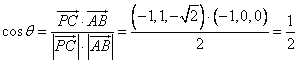 ,
,
则直线AB与平面ADE所成的角为![]() .
.
(3)因为![]() ,所以
,所以![]() ,
,

练习册系列答案
相关题目