题目内容
已知函数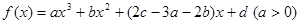 的图像如图所示,且
的图像如图所示,且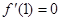 .则
.则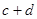 的值是 .
的值是 .
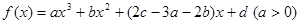 的图像如图所示,且
的图像如图所示,且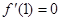 .则
.则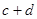 的值是 .
的值是 . 
3.
试题分析:因为
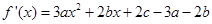 ,所以由
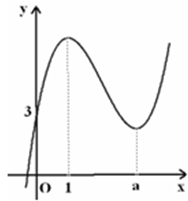
,所以由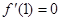 得c=0.由图可知f(0)=3可得d=3.所以c+d=3.故填3.本题看是字母参数很多,但关键是利用两个条件就可以求出需要的两个字母的值.图中标出
得c=0.由图可知f(0)=3可得d=3.所以c+d=3.故填3.本题看是字母参数很多,但关键是利用两个条件就可以求出需要的两个字母的值.图中标出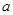 的位置在这里有迷惑的作用.
的位置在这里有迷惑的作用.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
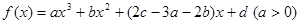 的图像如图所示,且
的图像如图所示,且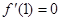 .则
.则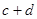 的值是 .
的值是 . 
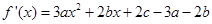 ,所以由
,所以由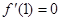 得c=0.由图可知f(0)=3可得d=3.所以c+d=3.故填3.本题看是字母参数很多,但关键是利用两个条件就可以求出需要的两个字母的值.图中标出
得c=0.由图可知f(0)=3可得d=3.所以c+d=3.故填3.本题看是字母参数很多,但关键是利用两个条件就可以求出需要的两个字母的值.图中标出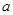 的位置在这里有迷惑的作用.
的位置在这里有迷惑的作用.
 阅读快车系列答案
阅读快车系列答案