题目内容
以下命题:
①对于任意向量
、
,都有|
•
|≥
•
成立;
②若首项a1<0,S9=S14,则前n项和Sn取得最小值时n值为11;
③已知a,b,b+a成等差数列,a,b,ab成等比数列,且
<logm(a+b)<1,则实数m的取值范围是(6,36);
④在锐角三角形ABC中,若A=2B,则
的取值范围是(
,
),
其中正确命题是
①对于任意向量
| a |
| b |
| a |
| b |
| a |
| b |
②若首项a1<0,S9=S14,则前n项和Sn取得最小值时n值为11;
③已知a,b,b+a成等差数列,a,b,ab成等比数列,且
| 1 |
| 2 |
④在锐角三角形ABC中,若A=2B,则
| b |
| a |
| 2 |
| 3 |
其中正确命题是
①③
①③
(填正确命题的番号)分析:利用所学的知识逐个判定命题是否正确,从而选出正确的命题.
解答:解:①当
、
夹角小于等于90°时,
•
≥0,此时|
•
|=
•
,
当
、
夹角大于90°时,
•
<0,此时|
•
|=-
•
>
•
,故①正确;
②∵S9=S14,∴s14-s9=a10+a11+a12+a13+a14=0,
又a1<0,{an}不是等差数列,不能得出Sn取得最小值时n=11,②不正确;
③∵a,b,b+a成等差数列,且a,b,ab成等比数列,∴
,解得a=2,b=4,∴a+b=6;
∴由
<logm(a+b)<1,知
<logm6<1,∴m∈(6,36),③正确;
④锐角△ABC中,若A=2B,则
<B<
(因为B小于
时,C将为钝角;B大于
时,A将为钝角);
∴
<cosB<
,∴
<
<
;
由sinA=sin2B,得sinA=2sinBcosB,∴
=
=
,即
的取值范围是(
,
),∴④不正确;
故答案为:①③
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
当
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
②∵S9=S14,∴s14-s9=a10+a11+a12+a13+a14=0,
又a1<0,{an}不是等差数列,不能得出Sn取得最小值时n=11,②不正确;
③∵a,b,b+a成等差数列,且a,b,ab成等比数列,∴
|
∴由
| 1 |
| 2 |
| 1 |
| 2 |
④锐角△ABC中,若A=2B,则
| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
| π |
| 4 |
∴
| ||
| 2 |
| ||
| 2 |
| ||
| 3 |
| 1 |
| 2cosB |
| ||
| 2 |
由sinA=sin2B,得sinA=2sinBcosB,∴
| b |
| a |
| sinB |
| sinA |
| 1 |
| 2cosB |
| b |
| a |
| ||
| 3 |
| ||
| 2 |
故答案为:①③
点评:本题通过判断命题的真假考查了平面向量的数量积、数列的综合应用以及解三角形的知识,是易错题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 ,记
,记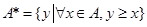 .设非空实数集合
.设非空实数集合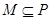 ,若
,若 时,则
时,则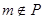 .
现给出以下命题:
.
现给出以下命题: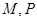 ,必有
,必有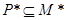 ;
;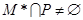 ;
; ;
;
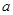 ,使得对任意的
,使得对任意的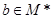 ,恒有
,恒有 ,
,