题目内容
以正方体ABCD-A1B1C1D1的顶点D为坐标原点O，如图，建立空间直角坐标系，则与
共线的向量的坐标可以是（ ）A．
B．
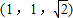
C．
D．
【答案】分析：设正方体的棱长为：1，由图形可知，B1点在正方体的上底面上，B1点的纵标同C的纵标相同，B1在面A1B1C1D1上，得到点的竖标为1，根据B1点在棱上的位置，写出B1点的横标，从而得到的B1坐标，最后写出向量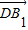
的坐标及与
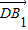共线的向量的坐标即可．
解答：解：由图形可知，B1点在正方体的上底面上，
设正方体的棱长为：1，
∴B1点的坐标是（1，1，1）
则与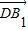
共线的向量的坐标可以是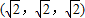
故选C．
点评：本题考查共线向量、空间中点的坐标，是一个基础题，解题时借助于点在正方体的一条棱上，写出横标，纵标和竖标，注意各个坐标的符号．
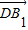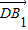的坐标及与共线的向量的坐标即可．解答：解：由图形可知，B1点在正方体的上底面上，
设正方体的棱长为：1，
∴B1点的坐标是（1，1，1）
则与
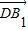共线的向量的坐标可以是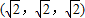故选C．
点评：本题考查共线向量、空间中点的坐标，是一个基础题，解题时借助于点在正方体的一条棱上，写出横标，纵标和竖标，注意各个坐标的符号．
练习册系列答案
相关题目
以正方体ABCD-A1B1C1D1的顶点D为坐标原点O，如图，建立空间直角坐标系，则与| DB1 |
A、(1，
| ||||||
B、(1，1，
| ||||||
C、(
| ||||||
D、(
|
B.
D.