Question

（本小题满分12分）一个多面体的直观图

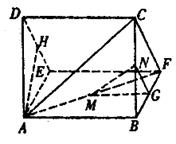
及三视图如图所示：（其中M、N分别是AF、BC的中点）. 

（Ⅰ）求证：MN∥平面CDEF； 

 （II）求多面体A—CDEF的体积.

Answer 1

（II）

解析:

（Ⅰ）由三视图可知，该多面体是底面为直

    角三角形的直三棱住ADE—BCF，……2分

    且AB=BC=BF=2，DE=CF=2

    ∴∠CBF=4分

取BF中点G，连MG、NG，由M、N分别为AF、

BC   的中点可得，NG∥CF，MG∥EF， 6分

    ∴平面MNG∥平面CDEF.   ∴MN∥平面CDEF.……8分

   （II）取DE的中点H.∵AD=AE，∴AH⊥DE，

在直三棱柱ADE—BCF中， 平面ADE⊥平面CDEF，

面ADE∩面CDEF=DE.∴AH⊥平面CDEF.…10分

∴多面体A—CDEF是以AH为高，以矩形CDEF为底面的棱锥，

在△ADE中，AH=，

∴棱锥A—CDEF的体积为……12分