题目内容
已知二次函数![]() .
.
(1)若![]() ,试判断函数
,试判断函数![]() 零点个数;
零点个数;
(2)若对![]() 且
且![]() ,
,![]() ,试证明
,试证明![]() ,使
,使![]() 成立。
成立。
(3)是否存在![]() ,使
,使![]() 同时满足以下条件①对
同时满足以下条件①对![]() ,且
,且![]() ;②对
;②对![]() ,都有
,都有![]() 。若存在,求出
。若存在,求出![]() 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
(1)函数![]() 有一个零点;当
有一个零点;当![]() 时,
时,![]() ,函数
,函数![]() 有两个零点。
有两个零点。
(2)证明见解析。
(3)![]() ,
,
解析:
(1)![]()
![]()
![]() 当
当![]() 时
时![]() ,
,
函数![]() 有一个零点;当
有一个零点;当![]() 时,
时,![]() ,函数
,函数![]() 有两个零点。………4分
有两个零点。………4分
(2)令![]() ,则
,则
![]()
![]() ,
,
![]()
![]()
在![]() 内必有一个实根。即
内必有一个实根。即![]() ,使
,使![]() 成立。
成立。
………………10分
(3)假设![]() 存在,由①知抛物线的对称轴为x=-1,且
存在,由①知抛物线的对称轴为x=-1,且![]()
∴![]()
![]()
![]()
由②知对![]() ,都有
,都有![]()
令![]() 得
得![]()
![]()
![]()
![]() ……………13分
……………13分
由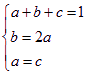 得
得![]() , ………………………………………………15分
, ………………………………………………15分
当![]() 时,
时,![]() ,其顶点为(-1,0)满足条件①,又
,其顶点为(-1,0)满足条件①,又![]()
![]() 对
对![]() ,都有
,都有![]() ,满足条件②。∴存在
,满足条件②。∴存在![]() ,使
,使![]() 同时满足条件①、②。…………………………16分
同时满足条件①、②。…………………………16分

练习册系列答案
相关题目
 在x=1处的导数值为1,则该函数的最大值是 (
)
在x=1处的导数值为1,则该函数的最大值是 (
)
 B.
B. C.
C. D.
D.
 。
。 的图像经过怎样平移得来;
的图像经过怎样平移得来;
 .
. ,试判断函数
,试判断函数 零点个数;
零点个数; 且
且 ,
, ,试证明
,试证明 ,使
,使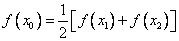 成立。
成立。 ,使
,使 同时满足以下条件①对
同时满足以下条件①对 ,且
,且 ;②对
;②对 ,都有
,都有 。若存在,求出
。若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。