题目内容
已知函数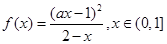 ,它的一个极值点是
,它的一个极值点是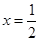 .
.
(Ⅰ) 求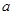 的值及
的值及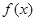 的值域;
的值域;
(Ⅱ)设函数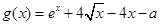 ,试求函数
,试求函数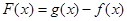 的零点的个数.
的零点的个数.
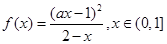 ,它的一个极值点是
,它的一个极值点是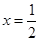 .
.(Ⅰ) 求
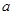 的值及
的值及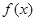 的值域;
的值域;(Ⅱ)设函数
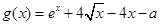 ,试求函数
,试求函数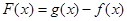 的零点的个数.
的零点的个数.(Ⅰ) 当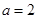 时,
时,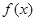 的值域为
的值域为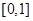 ;当
;当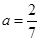 时,
时,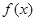 的值域为
的值域为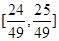 ;(Ⅱ) 当
;(Ⅱ) 当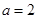 时,函数
时,函数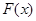 有2个零点;当
有2个零点;当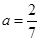 时,函数
时,函数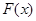 没有零点.
没有零点.
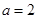 时,
时,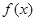 的值域为
的值域为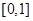 ;当
;当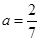 时,
时,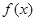 的值域为
的值域为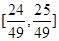 ;(Ⅱ) 当
;(Ⅱ) 当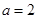 时,函数
时,函数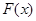 有2个零点;当
有2个零点;当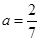 时,函数
时,函数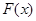 没有零点.
没有零点.试题分析:(Ⅰ)因为它的一个极值点是
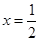 ,所以有
,所以有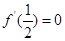 ,可求出
,可求出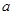 的值,从而求出值域;(Ⅱ) 函数
的值,从而求出值域;(Ⅱ) 函数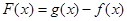 的零点个数问题可转化为函数
的零点个数问题可转化为函数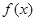 的图象与函数
的图象与函数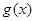 的图象的交点个数问题.
的图象的交点个数问题.试题解析:(1)
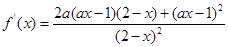 ,因为它的一个极值点是
,因为它的一个极值点是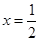 ,所以有
,所以有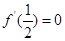 ,可得
,可得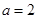 或
或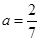 .当
.当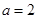 时,分析可知:
时,分析可知: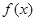 在区间
在区间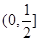 单调递减,在区间
单调递减,在区间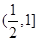 单调递增;由此可求得,
单调递增;由此可求得,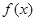 的值域为
的值域为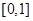 ;当
;当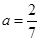 时,分析可知:
时,分析可知: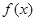 在区间
在区间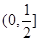 单调递减,在区间
单调递减,在区间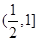 单调递增;由此可求得,
单调递增;由此可求得,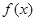 的值域为
的值域为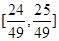 .
.(Ⅱ)函数
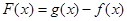 的零点个数问题可转化为函数
的零点个数问题可转化为函数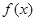 的图象与函数
的图象与函数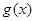 的图象的交点个数问题.
的图象的交点个数问题.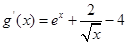 .因为
.因为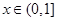 ,所以
,所以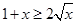 ,所以
,所以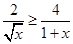 .设
.设 ,则
,则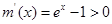 ,所以函数
,所以函数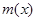 在区间
在区间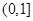 上单调递增,所以
上单调递增,所以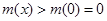 ,即有
,即有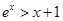 .所以
.所以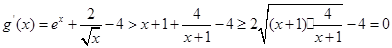 .所以,函数
.所以,函数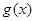 在区间
在区间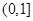 上单调递增.
上单调递增.(ⅰ)当
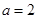 时,
时,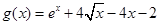 ,
,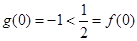 ,
,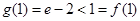 ,
,而
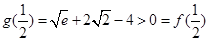 ,结合(1)中函数
,结合(1)中函数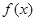 的单调性可得,此时函数
的单调性可得,此时函数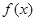 的图象与函数
的图象与函数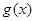 的图象有2个交点,即函数
的图象有2个交点,即函数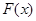 有2个零点.
有2个零点.(ⅱ)当
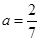 时,
时, ,由于
,由于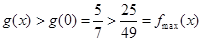 ,所以,此时函数
,所以,此时函数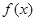 的图象与函数
的图象与函数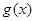 的图象没有交点,即函数
的图象没有交点,即函数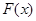 没有零点.
没有零点.综上所述,当
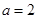 时,函数
时,函数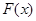 有2个零点;当
有2个零点;当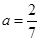 时,函数
时,函数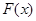 没有零点.
没有零点.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
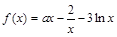 ,其中
,其中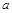 为常数.
为常数.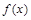 的图象在点
的图象在点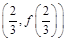 处的切线的斜率为1时,求函数
处的切线的斜率为1时,求函数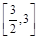 上的最小值;
上的最小值;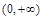 上既有极大值又有极小值,求实数
上既有极大值又有极小值,求实数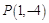 作函数
作函数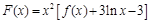 图象的切线,试问这样的切线有几条?并求这些切线的方程.
图象的切线,试问这样的切线有几条?并求这些切线的方程.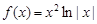 ,
,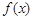 的奇偶性;
的奇偶性;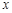 的方程
的方程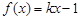 有实数解,求实数
有实数解,求实数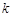 的取值范围
的取值范围 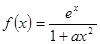 ,其中
,其中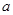 为正实数,
为正实数,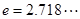 .
.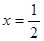 是
是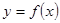 的一个极值点,求
的一个极值点,求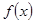 的单调区间.
的单调区间. ,其中
,其中 是常数且
是常数且 .
. 时,
时, 在区间
在区间 上单调递增,求
上单调递增,求 的取值范围;
的取值范围; 时,讨论
时,讨论 是正整数,证明:
是正整数,证明: .
.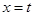 与函数
与函数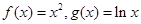 的图象分别交于点
的图象分别交于点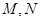 ,则当
,则当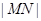 达到最小时
达到最小时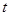 的值为( )
的值为( )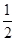
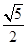
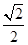
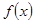 =
=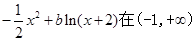 上是减函数,则
上是减函数,则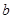 的取值范围是___________.
的取值范围是___________.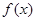 是定义在
是定义在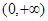 上的非负可导函数,且满足
上的非负可导函数,且满足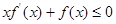 .对任意正数
.对任意正数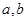 ,若
,若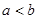 ,则必有( )
,则必有( )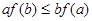
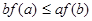
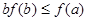
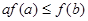
 .(1)求函数
.(1)求函数 的单调区间;
的单调区间; .若至少存在一个
.若至少存在一个 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.