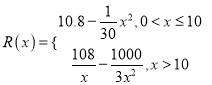题目内容
【题目】如图,在四棱锥![]() 中,已知底面
中,已知底面![]() 为平行四边形,
为平行四边形, ![]() ,三角形
,三角形![]() 为锐角三角形,面
为锐角三角形,面![]() 面
面![]() ,设
,设![]() 为
为![]() 的中点.
的中点.
求证: (1) ![]() 面
面![]() ;
;
(2) ![]() 面
面![]() .
.

【答案】(1)见解析(2)见解析
【解析】试题分析:(1)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,由三角形中位线定理可得
,由三角形中位线定理可得![]() //
// ![]() ,又
,又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() //平面
//平面![]() ;(2)过
;(2)过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,根据面面垂直的性质定理可得
,根据面面垂直的性质定理可得![]() 平面
平面![]() ,根据线面垂直的性质可得
,根据线面垂直的性质可得![]() ,结合
,结合![]() ,根据线面垂直的判定定理可得
,根据线面垂直的判定定理可得![]() 面
面![]() .
.
试题解析:(1)证明:连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
在平行四边形![]() 中,对角线
中,对角线![]() 交
交![]() 于
于![]() ,
,
则![]() 为
为![]() 的中点,又已知
的中点,又已知![]() 为
为![]() 的中点,所以
的中点,所以![]() 为
为![]() 的中位线,
的中位线,
所以![]() //
// ![]() ,又
,又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() //平面
//平面![]() .
.
(2)过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,即
,即![]() ;因为三角形
;因为三角形![]() 为锐角三角形,所以CM与CB不重合,因为,平面
为锐角三角形,所以CM与CB不重合,因为,平面![]()
![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]()
![]() ,且
,且![]() ,
, ![]() 平面
平面![]() ,所以,
,所以, ![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() ,又已知
,又已知![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
,
所以![]()
![]() 平面
平面![]() 。
。
【方法点晴】本题主要考查线面平行的判定定理、线面垂直的判定定理,属于难题. 证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案【题目】如今我们的互联网生活日益丰富,除了可以很方便地网购,网上叫外卖也开始成为不少人日常生活中不可或缺的一部分,为了解网络外卖在![]() 市的普及情况,
市的普及情况, ![]() 市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到表格(单位:人).
市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到表格(单位:人).

(1)根据表中数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用网络外卖的情况与性别有关?
市使用网络外卖的情况与性别有关?
(2)①现从所抽取的女网民中利用分层抽样的方法再抽取5人,再从这5人中随机选出了3人赠送外卖优惠券,求选出的3人中至少有2人经常使用网络外卖的概率;
②将频率视为概率,从![]() 市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为
市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】在对人们休闲方式的一次调查中,共调查120人,其中女性70人,男性50人.女性中有40人主要的休闲方式是看电视,另外30人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外30人主要的休闲方式是运动.
(1)根据以上数据建立一个2×的列联表:
休闲方式 性别 | 看电视 | 运 动 | 总 计 |
女 性 | |||
男 性 | |||
总 计 |
(2)有多大的把握认为休闲方式与性别有关?
参考公式及数据:K2=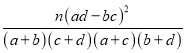
①当K2>2.706时,有90%的把握认为A、B有关联;
②当K2>3.841时,有95%的把握认为A、B有关联;
③当K2>6.635时,有99%的把握认为A、B有关联.