题目内容
15.在平面直角坐标系xOy中,设M是由不等式组$\left\{\begin{array}{l}{(\sqrt{3}x+y)(\sqrt{3}x-y)≥0}\\{y≥0}\end{array}\right.$表示的区域,A是到原点的距离不大于1的点构成的区域,向A中随机投一点,则所投点落在M中的概率是$\frac{1}{3}$.分析 本题属于几何概型,利用“测度”求概率,本例的测度即为区域的面积,故只要求出题中两个区域:由不等式组$\left\{\begin{array}{l}{(\sqrt{3}x+y)(\sqrt{3}x-y)≥0}\\{y≥0}\end{array}\right.$表示的落在圆内的面积区域和到原点的距离不大于1的点构成的区域的面积后再求它们的比值即可.
解答  解:根据题意可得,A是到原点的距离不大于1的点构成的区域,表示以原点为圆心,以1为半径的圆及其内部,面积为S1=π,
解:根据题意可得,A是到原点的距离不大于1的点构成的区域,表示以原点为圆心,以1为半径的圆及其内部,面积为S1=π,
点M(x,y)满足$\left\{\begin{array}{l}{(\sqrt{3}x+y)(\sqrt{3}x-y)≥0}\\{y≥0}\end{array}\right.$,
其构成的区域D如图所示,落在圆内的面积为S2=$\frac{π}{3}$,
所以所求的概率为P=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题主要考查几何概型.几何概型的特点是:实验结果的无限性和每一个实验结果出现的等可能性.在具体问题的研究中,要善于将基本事件“几何化”,构造出随机事件对应的几何图形,抓住其直观性,把握好几何区域的“测度”,利用“测度”的比来计算几何概型的概率.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
20.圆心在(1,-2),半径为2$\sqrt{5}$的圆在x轴上截得的弦长等于( )
| A. | 4$\sqrt{3}$ | B. | 6 | C. | 6$\sqrt{2}$ | D. | 8 |
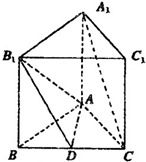 如图:正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1.
如图:正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1. 统计甲、乙两名篮球运动员在10场比赛得分,并绘制成如图所示的茎叶图,则甲、乙两位运动员得分数据中位数之差的绝对值是( )
统计甲、乙两名篮球运动员在10场比赛得分,并绘制成如图所示的茎叶图,则甲、乙两位运动员得分数据中位数之差的绝对值是( )