题目内容
求下列函数的值域:
(1)y=3x2-x+2; (2)y=
; (3)y=
;
(4)y=x+4
; (5)y=x+
; (6)y=|x-1|+|x+4|;
(7)y=
; (8)y=
(x>
); (9)y=
(10)y=
; (11)y=2x+4
; (12)y=-
(13)y=4-
;(14)y=x-
;(15)y=
.
(1)y=3x2-x+2; (2)y=
| -x2-6x-5 |
| 3x+1 |
| x-2 |
(4)y=x+4
| 1-x |
| 1-x2 |
(7)y=
| 2x2-x+2 |
| x2+x+1 |
| 2x2-x+1 |
| 2x-1 |
| 1 |
| 2 |
| 1-sinx |
| 2-cosx |
(10)y=
| x2-5x+6 |
| x2+x-6 |
| 1-x |
| x | ||
|
(13)y=4-
| 3+2x-x2 |
| 1-2x |
| 2x2+2x+5 |
| x2+x+1 |
分析:(1)利用二次函数的性质,结合函数图象可求
(2)要求原函数的值域,转化为求二次函数-x2-6x-5的值域问题的求解,基本方法是配方
((3)把函数化简y=
=
=3+
,结合反比例函数的性质可求
(4)利用换元法,然后结合二次函数的性质可求函数的值域.
(5)利用换元,令x=cosα,然后由辅助角公式,结合正弦函数的性质可求
(6)利用分段函数进行讨论,把函数化简为y=|x-1|+|x+4|=
,从而可求
(7)利用判别式法进行求解
(8)由y=
,分离系数后利用基本不等式求解函数的值域
(9)由于y=
=
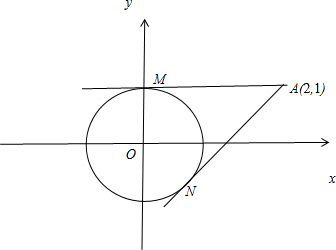
可以看着在单位圆上任取一点与定点A(2,1)的连线的斜率,根据几何意义可求函数的值域
(10)利用分离系数法,结合反比例函数的值域进行求解
(11)利用换元,结合二次函数的配方法进行求解
(12)分x>0,x=0,x<0三种情况,分子分母同时x,然后结合二次函数的配方法进行求解
(13)利用二次函数的配方法进行求解函数的值域
(14)利用函数的单调性进行求解函数的值域
(15)利用分离系数法,然后由二次函数的值域的求解的配方法进行求解
(2)要求原函数的值域,转化为求二次函数-x2-6x-5的值域问题的求解,基本方法是配方
((3)把函数化简y=
| 3x+1 |
| x-2 |
| 3(x-2)+7 |
| x-2 |
| 7 |
| x-2 |
(4)利用换元法,然后结合二次函数的性质可求函数的值域.
(5)利用换元,令x=cosα,然后由辅助角公式,结合正弦函数的性质可求
(6)利用分段函数进行讨论,把函数化简为y=|x-1|+|x+4|=
|
(7)利用判别式法进行求解
(8)由y=
(x-
| ||||||||
x-
|
(9)由于y=
| 1-sinx |
| 2-cosx |
| sinx-1 |
| cosx-2 |
(10)利用分离系数法,结合反比例函数的值域进行求解
(11)利用换元,结合二次函数的配方法进行求解
(12)分x>0,x=0,x<0三种情况,分子分母同时x,然后结合二次函数的配方法进行求解
(13)利用二次函数的配方法进行求解函数的值域
(14)利用函数的单调性进行求解函数的值域
(15)利用分离系数法,然后由二次函数的值域的求解的配方法进行求解
解答:解(1)y=3x2-x+2
由二次函数的性质可知,当x=
时,函数有最小值
故函数的值域为[
,+∞)
(2)y=
=
∵0≤
≤
0
∴0≤y≤2
故函数的值域[0,2]
(3)y=
=
=3+
≠3
故函数的值域(-∞,3)∪(3,+∞)
(4)令
=t则t≥0且x=1-t2
y=x+4
=1-t2+4t=-(t-2)2+5在[0,2]上单调递增,在[2,+∞)单调递减
当t=2时,函数有最大值5
∴函数的值域为(-∞,5]
(5)令x=cosα,则y=x+
=cosα+sinα=
sin(α+
)
∴-
y≤
(6)y=|x-1|+|x+4|=
∴y≥5
故函数的值域[5,+∞)
(7)∵y=
∴(y-2)x2+(y+1)x+y-2=0
①当y=2时,x=0满足条件
②当y≠2时,△=(y+1)2-4(y-2)2≥0即y2-6y+5≤0
解可得1≤y≤5且y≠2
综上可得,1≤y≤5
故函数的值域为{y|1≤y≤5}
(8)∵x>
∴x-
>0
∴x-
+
≥2
=
∴y=
=x+
+
+
≥
+
故函数的值域为[
+
,+∞)
(9)∵y=
=
可以看着在单位圆上任取一点与定点A(2,1)的连线的斜率
当直线与圆相切时,由圆心到直线的距离为半径可得斜率k=0或k=
∴0≤k≤
故函数的值域为[0,
]
(10)∵y=
=
=
(x≠2)
∴y=
=
1-
∴y≠-
且y≠1
∴函数的值域为{y|y≠1且y≠-
}
(11)∵y=2x+4
令
=t,则x=1-t2且t≥0
∴y=2x+4
=2(1-t2)+4t=-2t2+4t+2=-2(t-1)2+4
根据二次函数的 性质可知,当t=1时,函数有最大值4
函数的值域为(-∞,4]
(12)y=-
①当x=0时,y=0
②当x>0,y=-
=-
=-
∵
+
+1=2(
+
)2+
>1
∴y>-1
③当x<0时,y=-
=
∵
+
+1=2(
+
)2+
≥
∴y≤
综上可得,函数的值域为R
(13)∵y=4-
的定义域[-1,3]
令f(x)=-x2+2x+3=-(x-1)2+4
则0≤f(x)≤4
∴0≤
≤2
∴2≤f(x)≤4即函数的值域[2,4]
(14)∵y=x-
的定义域为(-∞,
],且在(-∞,
]上单调递增
∴当x=
时,函数有最大值
故函数的值域(-∞,
]
(15)∵y=
∴(y-2)x2-(y-2)x+y-5=0
∴△=(y-2)2-4(y-2)(y-5)≥0
即(y-2)(3y-18)≤0
∴2≤y≤6
故函数的值域(2,6]
由二次函数的性质可知,当x=
| 1 |
| 6 |
| 23 |
| 12 |
故函数的值域为[
| 23 |
| 12 |
(2)y=
| -x2-6x-5 |
| -(x+3)2+4 |
∵0≤
| -(x+3)2+4 |
| 4 |
∴0≤y≤2
故函数的值域[0,2]
(3)y=
| 3x+1 |
| x-2 |
| 3(x-2)+7 |
| x-2 |
| 7 |
| x-2 |
故函数的值域(-∞,3)∪(3,+∞)
(4)令
| 1-x |
y=x+4
| 1-x |
当t=2时,函数有最大值5
∴函数的值域为(-∞,5]
(5)令x=cosα,则y=x+
| 1-x2 |
| 2 |
| π |
| 4 |
∴-
| 2≤ |
| 2 |
(6)y=|x-1|+|x+4|=
|
∴y≥5
故函数的值域[5,+∞)
(7)∵y=
| 2x2-x+2 |
| x2+x+1 |
∴(y-2)x2+(y+1)x+y-2=0
①当y=2时,x=0满足条件
②当y≠2时,△=(y+1)2-4(y-2)2≥0即y2-6y+5≤0
解可得1≤y≤5且y≠2
综上可得,1≤y≤5
故函数的值域为{y|1≤y≤5}
(8)∵x>
| 1 |
| 2 |
| 1 |
| 2 |
∴x-
| 1 |
| 2 |
| ||
x-
|
(x-
|
| 2 |
∴y=
(x-
| ||||||||
x-
|
| 1 |
| 2 |
| ||
x-
|
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
故函数的值域为[
| 2 |
| 1 |
| 2 |
(9)∵y=
| 1-sinx |
| 2-cosx |
| sinx-1 |
| cosx-2 |
当直线与圆相切时,由圆心到直线的距离为半径可得斜率k=0或k=
| 4 |
| 3 |
∴0≤k≤
| 4 |
| 3 |
故函数的值域为[0,
| 4 |
| 3 |

(10)∵y=
| x2-5x+6 |
| x2+x-6 |
| (x-2)(x-3) |
| (x+3)(x-2) |
| x-3 |
| x+3 |
∴y=
| x-3 |
| x+3 |
| x+3-6 |
| x+3 |
| 6 |
| x+3 |
∴y≠-
| 1 |
| 5 |
∴函数的值域为{y|y≠1且y≠-
| 1 |
| 5 |
(11)∵y=2x+4
| 1-x |
令
| 1-x |
∴y=2x+4
| 1-x |
根据二次函数的 性质可知,当t=1时,函数有最大值4
函数的值域为(-∞,4]
(12)y=-
| x | ||
|
①当x=0时,y=0
②当x>0,y=-
| x | ||
|
| 1 | ||||
|
| 1 | ||||||
|
∵
| 2 |
| x2 |
| 2 |
| x |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
∴y>-1
③当x<0时,y=-
| x | ||
|
| 1 | ||||||
|
∵
| 2 |
| x2 |
| 2 |
| x |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴y≤
| 2 |
综上可得,函数的值域为R
(13)∵y=4-
| 3+2x-x2 |
令f(x)=-x2+2x+3=-(x-1)2+4
则0≤f(x)≤4
∴0≤
| 3+2x-x2 |
∴2≤f(x)≤4即函数的值域[2,4]
(14)∵y=x-
| 1-2x |
| 1 |
| 2 |
| 1 |
| 2 |
∴当x=
| 1 |
| 2 |
| 1 |
| 2 |
故函数的值域(-∞,
| 1 |
| 2 |
(15)∵y=
| 2x2+2x+5 |
| x2+x+1 |
∴(y-2)x2-(y-2)x+y-5=0
∴△=(y-2)2-4(y-2)(y-5)≥0
即(y-2)(3y-18)≤0
∴2≤y≤6
故函数的值域(2,6]
点评:本题主要考查了函数值域求解的一些常用方法的应用,要注意配方、换元、函数的单调性、判别式法、及利用几何意义等方法的应用

练习册系列答案
相关题目