题目内容
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(2)证明:当![]() 时,不等式
时,不等式![]() 在
在![]() 上恒成立.
上恒成立.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)由题意得出![]() 对任意的
对任意的![]() 恒成立,利用参变量分离法得出
恒成立,利用参变量分离法得出![]() 在
在![]() 上恒成立.构造函数
上恒成立.构造函数![]() ,利用导数求出函数
,利用导数求出函数![]() 的最小值,由此可得出实数
的最小值,由此可得出实数![]() 的取值范围;
的取值范围;
(2)分![]() 和
和![]() 来证明不等式
来证明不等式![]() 成立,在
成立,在![]() 时显然成立,在
时显然成立,在![]() 时,可考虑证
时,可考虑证![]() ,即证
,即证![]() ,构造函数
,构造函数![]() ,利用导数分析函数
,利用导数分析函数![]() 的单调性与最值,即可得证.
的单调性与最值,即可得证.
(1)因为![]() ,所以
,所以![]() .
.
因为函数![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立.
上恒成立.
令![]() ,则
,则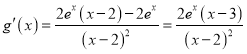 ,
,
所以当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,函数
,函数![]() 单调递增.
单调递增.
所以![]() ,所以
,所以![]() ,即
,即![]() ,
,
故![]() 的取值范围为
的取值范围为![]() ;
;
(2)显然,当![]() 时,
时,![]() 在
在![]() 上恒成立.
上恒成立.
当![]() 时,
时,![]() ,所以可考虑证
,所以可考虑证![]() ,即证
,即证![]() .
.
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,即函数
,即函数![]() 在
在![]() 上单调递增,
上单调递增,
所以当![]() 时,
时,![]() ,
,
所以当![]() 时,
时,![]() .
.
综上,当![]() 时,不等式
时,不等式![]() 在
在![]() 上恒成立.
上恒成立.

【题目】海南盛产各种名贵树木,如紫檀、黄花梨等.在实际测量单根原木材体积时,可以检量木材的实际长度(检尺长)和小头直径(检尺径),再通过国家公布的原木材积表直接查询得到,原木材积表的部分数据如下所示:
检尺径 ( | 检尺长( | ||||
2.0 | 2.2 | 2.4 | 2.5 | 2.6 | |
材积( | |||||
8 | 0.0130 | 0.0150 | 0.0160 | 0.0170 | 0.0180 |
10 | 0.0190 | 0.0220 | 0.0240 | 0.0250 | 0.0260 |
12 | 0.0270 | 0.0300 | 0.0330 | 0.0350 | 0.0370 |
14 | 0.0360 | 0.0400 | 0.0450 | 0.0470 | 0.0490 |
16 | 0.0470 | 0.0520 | 0.0580 | 0.0600 | 0.0630 |
18 | 0.0590 | 0.0650 | 0.0720 | 0.0760 | 0.0790 |
20 | 0.0720 | 0.0800 | 0.0880 | 0.0920 | 0.0970 |
22 | 0.0860 | 0.0960 | 0.1060 | 0.1110 | 0.1160 |
24 | 0.1020 | 0.1140 | 0.1250 | 0.1310 | 0.1370 |
若小李购买了两根紫檀原木,一根检尺长为![]() ,检尺径为
,检尺径为![]() ,另一根检尺长为
,另一根检尺长为![]() ,检尺径为
,检尺径为![]() ,根据上表,可知两根原木的材积之和为______
,根据上表,可知两根原木的材积之和为______![]() .
.