题目内容
已知函数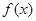 满足
满足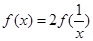 ,当
,当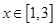 时,
时,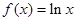 ,若在区间
,若在区间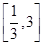 内,函数
内,函数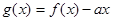 有三个不同零点,则实数
有三个不同零点,则实数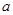 的取值范围是( )
的取值范围是( )
A.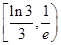 | B.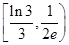 | C.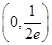 | D.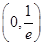 |
A
解析试题分析:在区间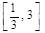 内,函数
内,函数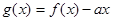 有三个不同的零点,
有三个不同的零点,
1)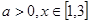 时,
时,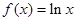 可得,
可得,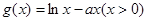 ,
,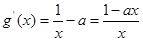
若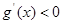 ,可得
,可得
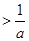 ,
,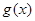 为减函数,
为减函数,
若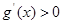 ,可得
,可得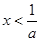 ,
,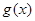 为增函数,
为增函数,
此时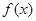 必须在
必须在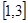 上有两个交点,
上有两个交点,
所以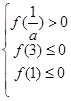 ,解得
,解得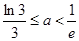
设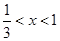 ,可得
,可得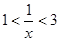 ,所以
,所以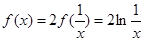 ,此时
,此时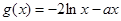 ,
,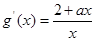 ,若
,若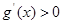 ,可得
,可得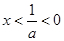 ,
,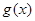 为增函数,
为增函数,
若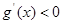 ,可得
,可得 ,
,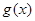 为减函数,在
为减函数,在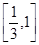 上有一个交点,则
上有一个交点,则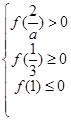 ,
,
解得
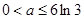
综上可得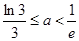
2)若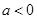 ,对于
,对于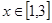 时,
时,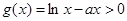 没有零点。综上
没有零点。综上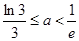
考点:利用导数研究函数的单调性;函数解析式的求解及常用方法;函数的零点.
点评:此题充分利用了分类讨论的思想,是一道综合题,难度比较大,需要排除a<0时的情况,注意解方程的计算量比较大,注意学会如何分类讨论;

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
 ,若
,若 ,则
,则 =( )
=( )
A. | B. | C. | D. |
若定义在R上的偶函数 满足
满足 ,且当
,且当 时,
时, ,则函数
,则函数 的零点的个数为
的零点的个数为
| A.8 | B.6 | C.5 | D.4 |
如果若干个函数的图象经过平移后能够重合,则称这些函数为“互为生成函数”。给出下列函数①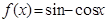 ;②
;②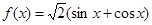 ;③
;③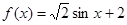 ;④
;④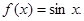 其中“互为生成函数”的是( )
其中“互为生成函数”的是( )
| A.①② | B.①③ | C.③④ | D.②④ |
设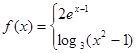
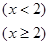 则
则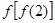 =( )
=( )
A.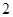 | B.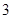 | C.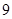 | D. |
下列函数中,满足 的是( )
的是( )
A. | B.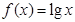 | C. | D. |
已知 ,
, ,则有:( )
,则有:( )
A. | B. |
C. | D.以上都不是 |
 时,在同一坐标系中,函数
时,在同一坐标系中,函数 与
与 的图象是
的图象是
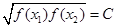 ,则称函数f(x)在D上的几何平均数为C.已知f(x)=x3,x∈[1,2],则函数f(x)=x3在[1,2]上的几何平均数为
,则称函数f(x)在D上的几何平均数为C.已知f(x)=x3,x∈[1,2],则函数f(x)=x3在[1,2]上的几何平均数为 B.2 C.4 D. 2
B.2 C.4 D. 2