题目内容
设函数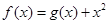 ,曲线
,曲线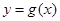 在点
在点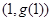 处的切线方程为
处的切线方程为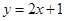 ,则曲线
,则曲线 在点
在点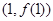 处切线的斜率为
处切线的斜率为
4
解析试题分析:先根据曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,可得g′(1)=2,再利用函数f(x)=g(x)+x2,可知f′(x)=g′(x)+2x,从而可求曲线y=f(x)在点(1,f(1))处切线的斜率.解:由题意,∵曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,∴g′(1)=2,∵函数f(x)=g(x)+x2,∴f′(x)=g′(x)+2x∴f′(1)=g′(1)+2∴f′(1)=2+2=4∴曲线y=f(x)在点(1,f(1))处切线的斜率为4,故答案为:4
考点:导数的几何意义
点评:本题考查的重点是曲线在点处切线的斜率,解题的关键是利用导数的几何意义.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 (单位:
(单位: )的作用下沿与力
)的作用下沿与力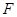 相同的方向,从
相同的方向,从 处运动到
处运动到 (单位:
(单位: )处,则力
)处,则力 做的功为 焦.
做的功为 焦.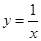 和直线
和直线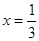 ,
,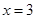 及
及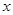 轴所围图形的面积为 .
轴所围图形的面积为 .
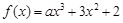 且
且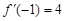 ,则实数
,则实数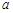 的值等于 ;
的值等于 ;  在
在 内有极小值,则实数
内有极小值,则实数 的取值范围
的取值范围 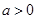 .若曲线
.若曲线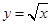 与直线
与直线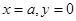 所围成封闭图形的面积为
所围成封闭图形的面积为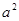 ,则
,则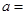 .
. 上的点
上的点 的切线方程为________________。
的切线方程为________________。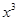 -x+3在点(1,3)处的切线方程为
-x+3在点(1,3)处的切线方程为