题目内容
已知函数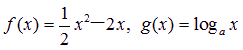 (a>0,且a≠1),其中为常数.如果
(a>0,且a≠1),其中为常数.如果![]() 是增函数,且
是增函数,且![]() 存在零点(
存在零点(![]() 为
为![]() 的导函数).
的导函数).
(Ⅰ)求a的值;
(Ⅱ)设A(x1,y1)、B(x2,y2)(x1<x2)是函数y=g(x)的图象上两点,![]() (
(![]() 为
为![]() 的导函数),证明:
的导函数),证明:![]() .
.
(1)a=e (2)证明略
解析:
(Ⅰ)因为![]()
![]() ,
,
所以![]() .…………………………3分
.…………………………3分
因为h(x)在区间![]() 上是增函数,
上是增函数,
所以![]() 在区间
在区间![]() 上恒成立.
上恒成立.
若0<a<1,则lna<0,于是![]() 恒成立.
恒成立.
又![]() 存在正零点,故△=(-2lna)2-4lna=0,lna=0,或lna=1与lna<0矛盾.
存在正零点,故△=(-2lna)2-4lna=0,lna=0,或lna=1与lna<0矛盾.
所以a>1.
由![]() 恒成立,又
恒成立,又![]() 存在正零点,故△=(-2lna)2-4lna=0,
存在正零点,故△=(-2lna)2-4lna=0,
所以lna=1,即a=e. ………………………………………7分
(Ⅱ)由(Ⅰ),![]() ,于是
,于是![]() ,
,![]() .…………9分
.…………9分
以下证明![]() . (※)
. (※)
(※)等价于![]() . ………………………11分
. ………………………11分
令r(x)=xlnx2-xlnx-x2+x,……………………………13分
r ′(x)=lnx2-lnx,在(0,x2]上,r′(x)>0,所以r(x)在(0,x2]上为增函数.
当x1<x2时,r(x1)< r(x2)=0,即![]() ,
,
从而![]() 得到证明.…………………………………………15分
得到证明.…………………………………………15分
对于![]() 同理可证
同理可证
所以![]() .……………………………………16分
.……………………………………16分

练习册系列答案
相关题目
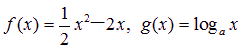 (a>0,且a≠1),其中为常数.如果
(a>0,且a≠1),其中为常数.如果 (a>0,且a≠1)
(a>0,且a≠1)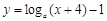 (a > 0,且
(a > 0,且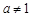 )的图象恒过定点A,若点A在直线
)的图象恒过定点A,若点A在直线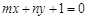 上,其中
上,其中 ,
,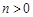 ,则
,则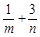 的最小值为__________.
的最小值为__________.