题目内容
设a是不等于1的正实数,z=x+yi(x、y∈R).规定z*=ax(cosy+isiny),?(1)求证:(z+2πi)*=z*;?
(2)设z1、z2为两个复数,试证明(z1+z2)*=z1*·z2*;?
(3)类比(2)的结论写出(z1-z2)*的有关运算式子,并证明你的结论.
证明:(1)∵z+2πi=x+(y+2π)i,?
∴(z+2πi)*=ax［cos(y+2π)+isin(y+2π)］??
=ax(cosy+isiny)=z*得证.?
(2)设z1=x1+y1i,z2=x2+y2i,z1+z2=x1+x2+(y1+y2)i.??
(z1+z2)*=ax1x2［cos(y1+y2)+isin(y1+y2）］,?
z1*·z2*=ax1(cosy1+isiny1)·ax2(cosy2+isiny2)?
=ax1+x2［cos(y1+y2)+isin(y1+y2）］.?
∴（z1+z2)*=z1*·z2*.?
(3)类比得(z1-z2)*=
.?
(z1-z2)*=ax1-x2［cos(y1-y2)+isin(y1-y2)］,?
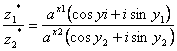=ax1-x2 
=ax1-x2［cos(y1-y2)+isin(y1-y2)］,得证.
练习册系列答案
智能训练练测考系列答案
相关题目
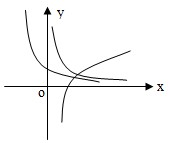
如图是函数f（x）=ax、g（x）=xb、h（x）=logcx（a、c是不等于1的正实数），则a、b、c的大小关系是（ ）
如图是函数f（x）=ax、g（x）=xb、h（x）=logcx（a、c是不等于1的正实数），则a、b、c的大小关系是
