题目内容
已知t＞0，关于x的方程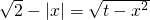
，则这个方程实根的个数不可能为
- A.4个
- B.3个
- C.2个
- D.1个
D
分析：由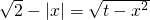≥0可得
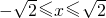，t≥x2，则可得
=
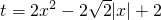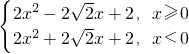，根据上述条件画出图象，结合函数的图象可求t的范围
解答：由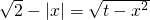≥0可得．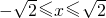
∵t≥x2
∴
∴=
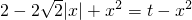
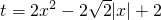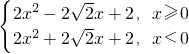
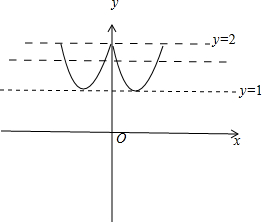
根据上述条件画出图象可知
（1）t=1时，方程有2个相异实数根
（2）1＜t＜2时，方程有4个相异实数根
（3）t=2时，方程有3个相异实数根
则方程实根的个数可能为2个或3个或4个，不可能为1个
故选D
点评：本题主要考查了函数的图象与方程的解的相互转化的思想的应用，解题的关键是准确作出函数的图象，体现了数形结合思想的应用
分析：由
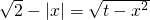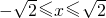≥0可得，t≥x2，则可得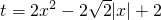=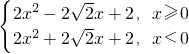，根据上述条件画出图象，结合函数的图象可求t的范围解答：由
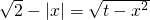≥0可得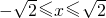．∵t≥x2
∴
∴
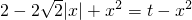
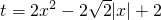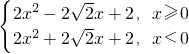
= 根据上述条件画出图象可知
（1）t=1时，方程有2个相异实数根
（2）1＜t＜2时，方程有4个相异实数根
（3）t=2时，方程有3个相异实数根
则方程实根的个数可能为2个或3个或4个，不可能为1个
故选D
点评：本题主要考查了函数的图象与方程的解的相互转化的思想的应用，解题的关键是准确作出函数的图象，体现了数形结合思想的应用
练习册系列答案
阅读快车系列答案
相关题目
，则这个方程有相异实根的个数情况是 ．