题目内容
已知a、b是两条异面直线,a⊥b,点P∉a且P∉b.下列命题中:
①在上述已知条件下,平面α一定满足:P∈α,a∥α且b∥α;
②在上述已知条件下,存在平面α,使P∉α,a?α且b⊥α;
③在上述已知条件下,直线c一定满足:P∈c,a∥c且b∥c;
④在上述已知条件下,存在直线c,使P∉c,a⊥c且b⊥c.
正确的命题有
①在上述已知条件下,平面α一定满足:P∈α,a∥α且b∥α;
②在上述已知条件下,存在平面α,使P∉α,a?α且b⊥α;
③在上述已知条件下,直线c一定满足:P∈c,a∥c且b∥c;
④在上述已知条件下,存在直线c,使P∉c,a⊥c且b⊥c.
正确的命题有
②④
②④
(把所有正确的序号都填上).分析:构造正方体ABCD-A1B1C1D,利用正方体的几何特征,分别讨论四个答题是否成立,综合分析结果可得答案.
解答: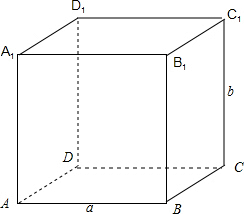 解:构造正方体ABCD-A1B1C1D,
解:构造正方体ABCD-A1B1C1D,
设AB所在的直线为a,CC1所在的直线为b,
当点P∈CD时,不存在平面α,使P∈α,a∥α且b∥α,故①错;
当点P∈C1D1时,存在平面ABCD为平面α,满足P∉α,a?α且b⊥α,故②正确;
当点P∈CD时,不存在直线c满足条件a∥c且b∥c,故③错;
当点P∈CD(不含C点)时,存在直线BC为直线c满足条件a⊥c且b⊥c,故④正确.
故正确的命题有:②④
故答案为:②④
 解:构造正方体ABCD-A1B1C1D,
解:构造正方体ABCD-A1B1C1D,设AB所在的直线为a,CC1所在的直线为b,
当点P∈CD时,不存在平面α,使P∈α,a∥α且b∥α,故①错;
当点P∈C1D1时,存在平面ABCD为平面α,满足P∉α,a?α且b⊥α,故②正确;
当点P∈CD时,不存在直线c满足条件a∥c且b∥c,故③错;
当点P∈CD(不含C点)时,存在直线BC为直线c满足条件a⊥c且b⊥c,故④正确.
故正确的命题有:②④
故答案为:②④
点评:本题以命题的真假判断与应用为载体考查了空间直线与平面的位置关系,本题比较抽象,判断难度比较大,故可引入正方体帮助分析.

练习册系列答案
相关题目
已知a、b是两条异面直线,c∥a,那么c与b的位置关系( )
| A、一定是异面 | B、不可能平行 | C、一定是相交 | D、不可能相交 |
 与圆
与圆 恒有公共点;
恒有公共点; 为△ABC的内角,则
为△ABC的内角,则 最小值为
最小值为 ;
; }中,
}中, 则使其前n项和
则使其前n项和 成立的最大正整数为2013;
成立的最大正整数为2013;