题目内容
4.已知不等式组$\left\{\begin{array}{l}{x-y≥0}\\{x+y≥0}\\{x≤2}\end{array}\right.$所表示的区域为D,|y|=x与|y|=$\frac{1}{2}$x2所围成的区域为M,现随机向区域D内抛一粒豆子,则豆子落在区域M的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 由题意画出图形,利用定积分求出阴影部分的面积,代入几何概型概率公式得答案.
解答  解:由题意作出平面区域D与M如图,
解:由题意作出平面区域D与M如图,
${S}_{△OAB}=\frac{1}{2}×2×4=4$,
阴影部分的面积为4-2${∫}_{0}^{2}\frac{1}{2}{x}^{2}dx$=$4-2×\frac{1}{6}{x}^{3}{|}_{0}^{2}$=$4-\frac{8}{3}=\frac{4}{3}$.
∴豆子落在区域M的概率为P=$\frac{\frac{4}{3}}{4}=\frac{1}{3}$.
故选:B.
点评 本题考查简单的线性规划,考查了几何概型概率的求法,训练了利用定积分求曲边梯形的面积,属中档题.

练习册系列答案
相关题目
15.设$\overrightarrow{a}$,$\overrightarrow{b}$为向量,且|$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$||$\overrightarrow{b}$|,那么( )
| A. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | B. | $\overrightarrow{a}$,$\overrightarrow{b}$同向 | C. | $\overrightarrow{a}$,$\overrightarrow{b}$反向 | D. | $\overrightarrow{a}$,$\overrightarrow{b}$平行 |
19.函数f(x)=sinx•ln|x|的图象大致是( )
| A. |  | B. |  | C. | 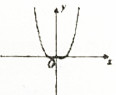 | D. |  |
 中,点
中,点 ,直线
,直线 ,设圆
,设圆 的半径为
的半径为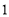 ,圆心在
,圆心在 上.
上.
 也在直线
也在直线 上,过点
上,过点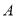 作圆
作圆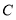 的切线,求切线的方程;
的切线,求切线的方程; ,使
,使 ,求圆心
,求圆心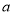 的取值范围.
的取值范围.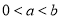 ,则下列不等式中正确的是
,则下列不等式中正确的是  B.
B.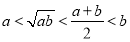
 D.
D.
 中,根据下列条件解三角形,则其中有二个解的是
中,根据下列条件解三角形,则其中有二个解的是 B.
B.
 D.
D.