题目内容
13.在三角形ABC中,已知AB=2,且$\frac{CA}{CB}$=2,则三角形ABC的面积的最大值为$\frac{4}{3}$.分析 设BC=a,则AC=2a,利用余弦定理可求得cos2B=$\frac{1}{{a}^{2}}+\frac{9{a}^{2}}{16}-\frac{3}{2}$,再利用三角形的面积公式可求得S△ABC=asinB,继而可求$({S}_{△ABC})^{2}$=-$\frac{9}{16}({a}^{2}-\frac{20}{9})^{2}+\frac{16}{9}$,从而可得△ABC面积的最大值.
解答 解:依题意,设BC=a,则AC=2a,又AB=2,
由余弦定理得:(2a)2=a2+22-4a•cosB,
即3a2+4acosB-4=0,
∴cosB=$\frac{1}{a}-\frac{3a}{4}$,
∴cos2B=$\frac{1}{{a}^{2}}+\frac{9{a}^{2}}{16}-\frac{3}{2}$,
∴sin2B=1-cos2B=$\frac{5}{2}-\frac{9{a}^{2}}{16}-\frac{1}{{a}^{2}}$,
∵S△ABC=$\frac{1}{2}$AB•BCsinB=$\frac{1}{2}$×2asinB=asinB,
∴$({S}_{△ABC})^{2}$=a2sin2B=a2($\frac{5}{2}-\frac{9{a}^{2}}{16}-\frac{1}{{a}^{2}}$)=-$\frac{9}{16}{a}^{4}+\frac{5}{2}{a}^{2}-1$
=-$\frac{9}{16}$(a4-$\frac{40{a}^{2}}{9}$)-1=-$\frac{9}{16}({a}^{2}-\frac{20}{9})^{2}+\frac{16}{9}$,
当a2=$\frac{20}{9}$,即a=$\frac{2\sqrt{5}}{3}$时,2、$\frac{2\sqrt{5}}{3}$、$\frac{4\sqrt{5}}{3}$能组成三角形,
∴$({S}_{△ABC}{)^{2}}_{max}=\frac{16}{9}$,
∴三角形ABC的面积的最大值为$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题考查余弦定理与正弦定理的应用,着重考查转化思想与二次函数的配方法,求得$({S}_{△ABC})^{2}$=-$\frac{9}{16}({a}^{2}-\frac{20}{9})^{2}+\frac{16}{9}$是关键,属于难题.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案| A. | -1 | B. | 1 | C. | 2 | D. | $\frac{5}{3}$ |
| A. | 第一、二象限 | B. | 第二象限 | C. | 第三、四象限 | D. | 以上都不对 |
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
 如图所示,角α的终边在图中阴影部分,试指出角α 的范围.
如图所示,角α的终边在图中阴影部分,试指出角α 的范围. 中
中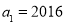 ,前
,前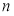 项和为
项和为 ,
,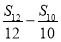
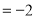 ,则
,则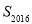 的值为__________.
的值为__________.