题目内容
已知动点P的轨迹为曲线C,且动点P到两个定点F1(-1,0),F2(1,0)的距离|| PF1 |
| PF2 |
| 2 |
(1)求曲线C的方程;
(2)直线l过圆x2+y2+4y=0的圆心Q与曲线C交于M,N两点,且
| ON |
| OM |
(3)设点A(1,
| 1 |
| 2 |
| PA |
| 2 |
| PF2 |
分析:(1)利用已知条件推断出|
|+|
|的值,进而求得椭圆方程中的长轴长,则a可求,利用定点坐标求得焦距,则b可求得,最后求得椭圆的方程.
(2)设出M,N的坐标,利用
•
=0(O判断出x1x2+y1y2=0设出直线l的方程代入椭圆的方程消去y,利用韦达定理表示出x1x2和x1+x2利用直线方程求得y1y2,代入x1x2+y1y2=0求得k,则直线l的方程可得.
(3)先利用椭圆的第二定义表示出到焦点与准线的距离求得点P到右准线的距离与|
|的关系式,进而推断出此时|
|+d的最小值为点A到右准线x=2的距离,则点P的坐标和最小距离可求得.
| PF1 |
| PF2 |
(2)设出M,N的坐标,利用
| ON |
| OM |
(3)先利用椭圆的第二定义表示出到焦点与准线的距离求得点P到右准线的距离与|
| PF2 |
| PA |
解答:解:(1)据已知|
|+|
|=2
,
所求曲线C是椭圆,长轴2a=2
,a=
,c=1,
所以椭圆的方程为
+y2=1.
(2)设M(x1,y1),N(x2,y2),
由
•
=0?x1x2+y1y2=0,
设l:y=kx-2,
y1=kx1-2,y2=kx2-2,y1y2=k2x1•x2-2k(x1+x2)+4,
(1+k2)x1x2-2k(x1+x2)+4=0(*).
联立
+y2=1,得x2+2(kx-2)2=2,
x1,x2为上述方程的两根,
∴x1x2=
,x1+x2=
代入(*)得k2=5?k=±
,
所求直线l为:
x-y-2=0或
x+y+2=0
(3)椭圆的右准线为x=2,设点P到右准线的距离为d,
则
=
?d=
|
|,|
|+
|
|=|
|+d,
此时|
|+d的最小值为点A到右准线x=2的距离,(|
|+d)min=1,
此时点P的坐标为(
,
).
| PF1 |
| PF2 |
| 2 |
所求曲线C是椭圆,长轴2a=2
| 2 |
| 2 |
所以椭圆的方程为
| x2 |
| 2 |
(2)设M(x1,y1),N(x2,y2),
由
| ON |
| OM |
设l:y=kx-2,
y1=kx1-2,y2=kx2-2,y1y2=k2x1•x2-2k(x1+x2)+4,
(1+k2)x1x2-2k(x1+x2)+4=0(*).
联立
| x2 |
| 2 |
x1,x2为上述方程的两根,
∴x1x2=
| 6 |
| 1+2k2 |
| 8k |
| 1+2k2 |
代入(*)得k2=5?k=±
| 5 |
所求直线l为:
| 5 |
| 5 |
(3)椭圆的右准线为x=2,设点P到右准线的距离为d,
则
|
| ||
| d |
| ||
| 2 |
| 2 |
| PF2 |
| PA |
| 2 |
| PF2 |
| PA |
此时|
| PA |
| PA |
此时点P的坐标为(
| ||
| 2 |
| 1 |
| 2 |
点评:本题主要考查了椭圆的简单性质,椭圆与直线的关系.考查了考生分析问题和解决问题的能力.

练习册系列答案
相关题目
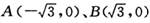 ,P为动点, 且
,P为动点, 且 .记动点P的轨迹为曲E
.记动点P的轨迹为曲E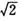 ,l与曲线E相交于不同的两点G、H, 问
,l与曲线E相交于不同的两点G、H, 问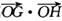 的值是否为定值?若为定值,求出此定值;
若不是, 请说明理由.
的值是否为定值?若为定值,求出此定值;
若不是, 请说明理由.