题目内容

已知向量a=3e1-2e2,b=4e1+e2,其中e1=(1,0),e2=(0,1).

求：（1）a·b;|a+b|;(2)a与b的夹角的余弦值.

解：(1)∵a=3e1-2e2=3(1,0)-2(0,1)=(3,0)-(0,2)=(3,-2)

b=4e1+e2=4(1,0)+(0,1)=(4,0)+(0,1)=(4,1).

则a·b=4×3+（-2）×1=10.

∵a+b=(7,-1).

∴|a+b|=

（2）设a·b的夹角为θ

则cosθ=.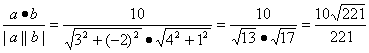

练习册系列答案
相关题目
已知向量
a
=3
e
1-2
e
2，
b
=4
e
1+
e
2，其中
e
1=（1，0），
e
2=（0，1），求：
（1）
a
•
b
和|
a
+
b
|的值；
（2）
a
与
b
夹角θ的余弦值．
已知向量
a
=3
e1
-2
e2
，
b
=4
e1
+
e2
，其中
e1
，
e2
是互相垂直的单位向量求：
（1）
a
•
b
，|
a
+
b
|；
（2）
a
与
b
夹角的余弦值．
已知向量
a
=3
e
1-2
e
2，
b
=4
e
1+
e
2，其中
e
1=（1，0），
e
2=（0，1），求：
（1）
a
•
b
和|
a
+
b
|的值；
（2）
a
与
b
夹角θ的余弦值．
已知向量
a
=3
e1
-2
e2
，
b
=4
e1
+
e2
，其中
e1
，
e2
是互相垂直的单位向量求：
（1）
a
•
b
，|
a
+
b
|；
（2）
a
与
b
夹角的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网